Το πρωτότυπο άρθρο δημοσιεύτηκε από το GIJN στις 21/4/2025 και αναδημοσιεύτηκε από το iMEdD κατόπιν άδειας. Η αναδημοσίευσή του απαιτεί άδεια από τον εκδότη.
Εξοπλισμοί: Το Ισραήλ και οι άλλοι
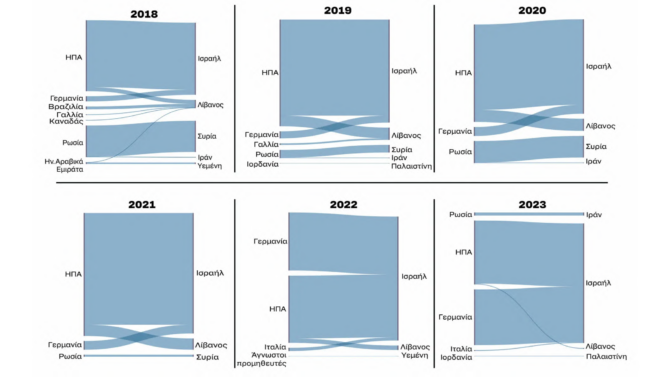
Τα δεδομένα του Stockholm International Peace Research Institute (SIPRI) για τις διεθνείς εξοπλιστικές προμήθειες προς Ισραήλ, Συρία, Ιράν, Λίβανο, Υεμένη και Παλαιστίνη. Τι δείχνουν τα στοιχεία για το ύψος των προμηθειών και την προέλευσή τους.
Ακόμα και οι πιο επιμελείς δημοσιογράφοι δεδομένων και ερευνητές-δημοσιογράφοι αφήνουν τα νούμερα να τους καταβάλλουν. Είναι υψίστης σημασίας να αποφεύγονται οι εσφαλμένοι υπολογισμοί και οι ανακρίβειες, αλλά εξίσου σημαντική είναι η προσεκτική παρουσίαση των αριθμών, με τρόπο που επιτρέπει στο αναγνωστικό κοινό να καταλάβει την ιστορία που αφηγούνται τα δεδομένα.
Συχνά αριθμητικά λάθη που κάνουν οι ερευνητές δημοσιογράφοι περιλαμβάνουν τον υπολογισμό ποσοστών προσθέτοντας ή αφαιρώντας από άλλες ποσοστιαίες τιμές. (Για παράδειγμα, μια πτώση των επιτυχημένων διώξεων από το 12% στο 7% δεν αποτελεί μείωση ύψους 5% αλλά περίπου 42%.) Αυτό το λάθος είναι τόσο συνηθισμένο που το Associated Press χρησιμοποιεί το σύμβολο % για τα ποσοστά, αλλά ζητά από τους δημοσιογράφους του να καταγράφουν «ποσοστιαίες μονάδες» όταν μετρούν μεταβολές, ώστε να προάγεται η μεγαλύτερη ακρίβεια και κατανόηση. Ένα ακόμα σοβαρό εννοιολογικό λάθος είναι η σύγχυση της συσχέτισης με την αιτιότητα. Το GIJN προσφέρει ενημερωτικά δελτία με συμβουλές για την αποφυγή σοβαρών αριθμητικών λαθών σε δημοσιογραφικά θέματα, όπως τα «10 Common Mistakes in Data Journalism» και «10 Simple Data Errors That Can Ruin an Investigation».
Εκτός αν υπάρχει ένας εξαιρετικά πειστικός λόγος, στρογγυλοποιήστε τους αριθμούς σας όπου είναι δυνατόν: αντί για “44.792”, πείτε “σχεδόν 45.000”.
Τζένιφερ Λα Φλερ, Μεταπτυχιακή Σχολή Δημοσιογραφίας του Μπέρκλεϊ
Όμως, ένα πάνελ στο πιο πρόσφατο συνέδριο δημοσιογραφίας δεδομένων NICAR 2025 πληροφόρησε το κοινό πως υπάρχουν μικρά αριθμητικά λάθη που διαφεύγουν από ερευνητές-δημοσιογράφους, τα οποία μπορούν να αλλοιώσουν την οπτική του θέματος και να κλονίσουν την εμπιστοσύνη των αναγνωστών. Οι εν λόγω ειδικές προειδοποίησαν, επίσης, πως, ακόμα και τεχνικά ακριβείς αριθμοί μπορούν, επίσης, να παραπλανήσουν ή να προκαλέσουν σύγχυση στο αναγνωστικό κοινό λόγω ακατάλληλων μορφοποιήσεων, υπερβολικά πολλών ψηφίων ή λόγω αποτυχίας στην απλοποίηση ή στην πλαισίωση των αριθμών αυτών για καλύτερη κατανόηση.
Σε αυτή τη συζήτηση στο NICAR συμμετείχαν η δημοσιογράφος δεδομένων Τζένιφερ Λα Φλερ (Jennifer LaFleur), η οποία διδάσκει οπτικοποίηση δεδομένων και μεθόδους έρευνας στη Μεταπτυχιακή Σχολή Δημοσιογραφίας του Μπέρκλεϊ, και η Τζέιμι Ντάουελ (Jaimi Dowdell), βραβευμένη δημοσιογράφος δεδομένων στο Reuters.
Οι δύο ομιλήτριες προσέφεραν τις ακόλουθες συμβουλές προς αποφυγή παραπληροφόρησης ή παραπλάνησης των αναγνωστών με τους αριθμούς:
Η παραπλανητική ακρίβεια μπορεί να οδηγήσει σε ανακρίβεια. Σίγουρα, θα πιστεύετε ότι στατιστικά στοιχεία όπως το «25,21% των γυναικών» είναι πιο ακριβή από το «μία στις τέσσερις γυναίκες». Παρόλα αυτά, η Λα Φλερ προειδοποιεί πως ακριβή νούμερα όπως το «25,21%» δεν είναι μόνο λιγότερο χρήσιμα για τους αναγνώστες, συγκριτικά με το «μία στις τέσσερις», αλλά μπορεί να αποτυπώνουν μια ακρίβεια που τα δεδομένα στην πραγματικότητα δεν υποστηρίζουν. «Νομίζω ότι μας αρέσει να προσθέτουμε δεκαδικά ψηφία γιατί μας κάνει να φαινόμαστε έξυπνοι, αλλά είναι δύσκολο για τον αναγνώστη να τα ερμηνεύσει», σημείωσε η Λα Φλερ. «Και μερικές φορές — αν τα δεδομένα που αναφέρετε έχουν περιθώριο σφάλματος — αυτά τα δεκαδικά ψηφία στην πραγματικότητα αποδίδουν εσφαλμένη ακρίβεια». Οι ειδικές, επίσης, επισημαίνουν ότι τα περισσότερα δεδομένα είναι παρωχημένα τη στιγμή που συγκεντρώνονται και, έτσι, η χρήση πολλών δεκαδικών σημείων μπορεί γενικά να παραπλανήσει το κοινό όσον αφορά την επάρκεια των δεδομένων τόσο των πηγών όσο και του θέματος. «Καλύτερα να πείτε “μία στις τέσσερις”, ή “σχεδόν οι μισές”, αν μπορείτε» πρόσθεσε. «Εκτός αν υπάρχει ένας εξαιρετικά πειστικός λόγος, στρογγυλοποιήστε τους αριθμούς σας όπου είναι δυνατόν: αντί για “44.792”, πείτε “σχεδόν 45.000”». Οι ειδικές δεδομένων στον οργανισμό Investigative Reporters and Editors (IRE) απέδειξαν τον κίνδυνο της ακρίβειας στους μέσους όρους με ακέραιους αριθμούς, υπολογίζοντας τους μισθούς των δασκάλων, προσαρμοσμένους στον πληθωρισμό, βάσει κυβερνητικών δεδομένων, στα 53.234 δολάρια — και, στη συνέχεια, υπολογίζοντας ξανά αυτόν τον μέσο όρο από τα ίδια δεδομένα ως 53.226 δολάρια, χρησιμοποιώντας έναν διαφορετικό αλλά εξίσου έγκυρο τύπο. Έτσι, στο τέλος, κατέληξαν ότι θα ήταν πιο σαφές, και όχι λιγότερο ακριβές, να στρογγυλοποιήσουν τον αριθμό στα 53.200 δολάρια.
Αποφύγετε τη φράση «φορές περισσότερο» για αυξήσεις αριθμών. Οι ρεπόρτερ συχνά ισχυρίζονται ότι, για παράδειγμα, 500 από κάτι είναι «πέντε φορές περισσότερα» από 100 από αυτά τα πράγματα. Στην πραγματικότητα, είναι μόνο τέσσερις φορές περισσότερα. (Θυμηθείτε πως 100% αύξηση οποιουδήποτε πράγματος σημαίνει πως έχει διπλασιαστεί ή ότι είναι «δύο φορές περισσότερο».) Αντίθετα, είναι πιο ακριβές να πούμε ότι η νέα τιμή είναι «πέντε φορές όσο» η αρχική τιμή. «Αυτό το βλέπω διαρκώς. Προτείνω να μη χρησιμοποιείτε τη λέξη “περισσότερο”, αλλά απλά να εξηγείτε πόσες φορές πολλαπλάσιο είναι, γιατί το “περισσότερο” μπερδεύει τους αναγνώστες» είπε η Λα Φλερ. Κάθε φορά που βλέπω “Χ φορές περισσότερο”, μαντεύω πως εννοούν πέντε φορές το ύψος, όχι πέντε φορές περισσότερο.
Μετακινήστε την υποδιαστολή για μικρούς αριθμούς. Οι ειδικές λένε ότι δεν υπάρχει τίποτα υποχρεωτικό ή μαγικό στη χρήση του «τοις εκατό» στα θέματα. Αν βοηθά τους αναγνώστες να καταλάβουν, σε μικρούς αριθμούς και στον βασικό τους αριθμό, οι δημοσιογράφοι έχουν την ελευθερία να μετακινήσουν την υποδιαστολή προς τα δεξιά — για παράδειγμα, μετατρέποντας έναν δείκτη ανθρωποκτονιών από 0,07% σε 70 ανθρωποκτονίες ανά 100.000 πληθυσμό.
Σιγουρευτείτε ότι διαβάζετε τα ψιλά γράμματα σε όλες τις βάσεις δεδομένων που παρέχουν πληροφορίες για το τι μπορείτε και δεν μπορείτε να κάνετε με τα νούμερα.
Τζέιμι Ντάουελ, δημοσιογράφος δεδομένων, Reuters
Κάντε τα πράγματα απλά όταν συγκρίνετε σχετικά μεγέθη. Το δίδυμο εξήγησε αυτή τη συμβουλή συγκρίνοντας το βάρος των αγαπημένων τους (τώρα θανόντων) γατιών — η γάτα της Ντάουελ, ο Amigo, ζύγιζε 10 κιλά, και η γάτα της Λα Φλερ, ο Stanley, ζύγιζε 5 κιλά. Η Ντάουελ παρατήρησε ότι, ενώ θα ήταν θεωρητικά αληθές να πει κανείς «Ο Amigo ήταν 100% βαρύτερος από τον Stanley» ή «Ο Amigo ζύγιζε 200% του βάρους του Stanley», προειδοποίησε ότι και οι δύο εκφράσεις θα ήταν ασαφείς για πολλούς αναγνώστες. Αντίθετα, το κοινό θα κατανοούσε πολύ καλύτερα αυτήν την απλούστερη δήλωση: «Ο Amigo ζύγιζε το διπλάσιο από τον Stanley».
Οι στρογγυλοποιημένοι αριθμοί μπορεί να είναι προειδοποιητικό «καμπανάκι». Η Ντάουελ προειδοποίησε πως καλά παρουσιασμένοι αριθμοί ή ποσοστά που είναι σωστά υπολογισμένα από μια κυβερνητική βάση δεδομένων ακριβείας, μπορούν και πάλι να είναι λάθος εξαιτίας περιορισμένου επιτρεπόμενου αριθμού λήψεων από την ιστοσελίδα, π.χ. έως 5.000 έγγραφα, στοιχείο που οι δημοσιογράφοι μπορεί να μην έχουν παρατηρήσει. «Σιγουρευτείτε ότι διαβάζετε τα ψιλά γράμματα σε όλες τις βάσεις δεδομένων που παρέχουν πληροφορίες για το τι μπορείτε και δεν μπορείτε να κάνετε με τα νούμερα», πρόσθεσε. «Γενικώς, προσέξτε τις στρογγυλοποιήσεις: οι υπερβολικά τέλειοι αριθμοί πρέπει να σας χτυπούν καμπανάκια».
Να θυμάστε ότι το «κατά κεφαλήν» σημαίνει απλώς ανά άτομο. Η Ντάουελ σημείωσε πως υπάρχει μια εντυπωσιακά συχνή παρεξήγηση για τη σημασία του όρου «κατά κεφαλήν», ο οποίος σημαίνει απλά «ανά άτομο». Η Λα Φλερ πρόσθεσε ότι, περιστασιακά, βλέπει δημοσιογραφικά θέματα να αναφέρονται σε παράλογα στατιστικά στοιχεία, όπως «300 ανθρωποκτονίες κατά κεφαλήν» σε μια κοινότητα. «Για τον λόγο αυτό, όταν έχουμε μικρούς αριθμούς, όπως για βίαια εγκλήματα ή κρούσματα σπάνιων ασθενειών, θα δείτε να γίνεται αναφορά ως ανά 10.000 ή 100.000 άτομα, ώστε να μπορείτε να δείτε τον απόλυτο αριθμό», πρόσθεσε.
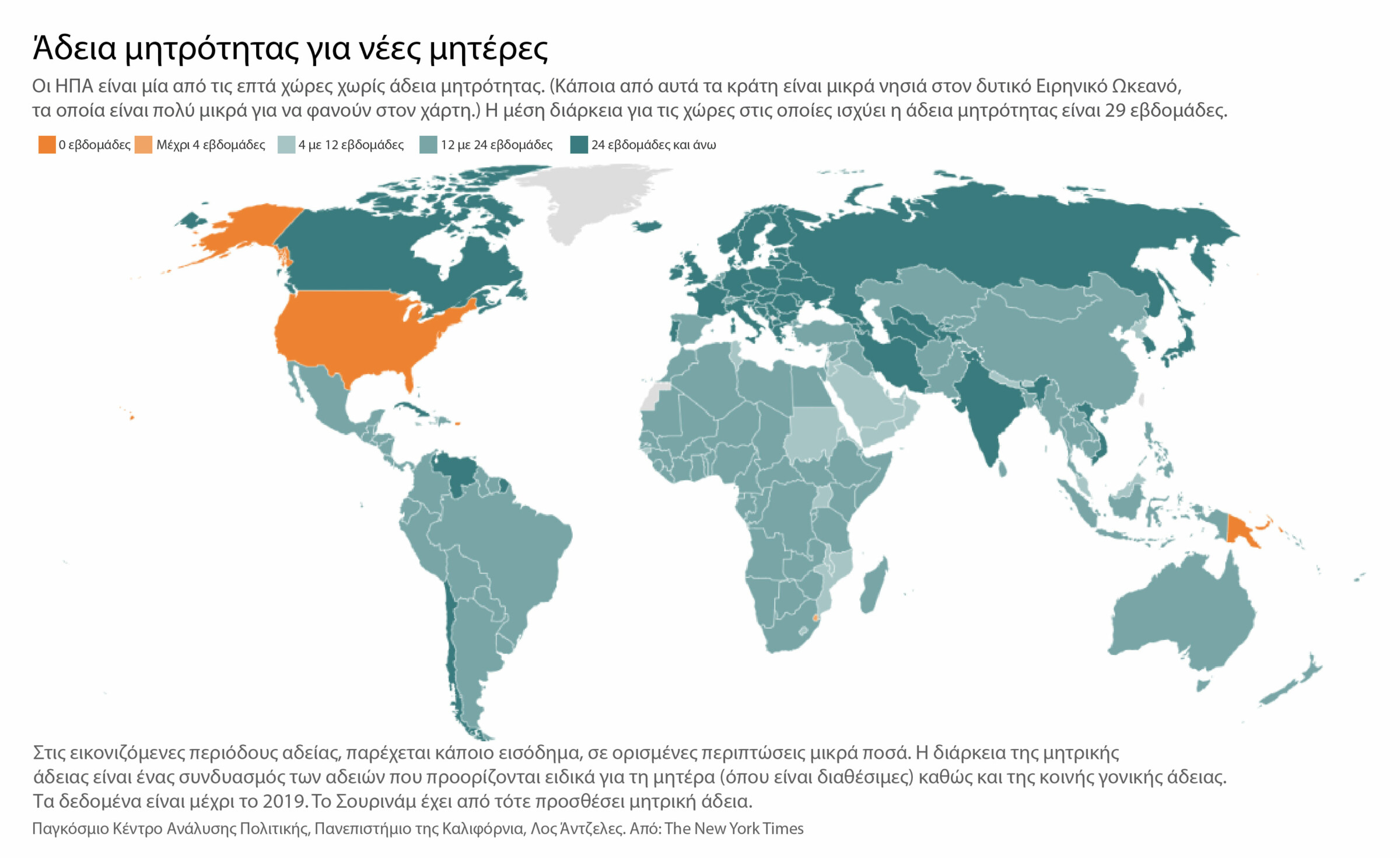
Χρησιμοποιήστε γραφήματα όταν οι αριθμοί δεν αποτυπώνουν την κλίμακα. Το στατιστικό που λέει ότι οι Ηνωμένες Πολιτείες είναι «μία από μόλις έξι χώρες χωρίς κρατικώς πληρωμένη άδεια μητρότητας» δεν αποδίδει επαρκώς την κλίμακα αυτής της εξαιρετικά σπάνιας πολιτικής. Αν και λιγότερο ενημερωτικό — καθώς οι τέσσερις από αυτές τις χώρες είναι νησιωτικά κράτη τόσο μικρά που δεν φαίνονται καν στον παγκόσμιο χάρτη — η Λα Φλερ σημείωσε ότι το ακόλουθο γράφημα των New York Times παρουσίασε το ζήτημα με έναν πιο ουσιαστικό και κατανοητό τρόπο για τους αναγνώστες.
Προσοχή στα δισεκατομμύρια και να δείχνετε την κλίμακα. Οι ειδικές σημειώνουν ότι οι αριθμοί σε δισεκατομμύρια χρησιμοποιούνται τόσο συχνά στα μέσα ενημέρωσης που τόσο οι δημοσιογράφοι όσο και οι αναγνώστες μπορεί να χάσουν την αίσθηση του πόσο τεράστιοι είναι. Μία συγκριτική αναλογία: ένα εκατομμύριο δευτερόλεπτα αντιστοιχούν σε μόλις 11 ημέρες, αλλά ένα δισεκατομμύριο δευτερόλεπτα ισούνται με σχεδόν 32 χρόνια. Είναι επίσης εκπληκτικά εύκολο να συγχέουμε τα εκατομμύρια με τα δισεκατομμύρια σε οικονομικές καταστάσεις. Η Ντάουελ ανέφερε μια πρόσφατη περίπτωση στην οποία ερευνητές δημοσιογράφοι παρατήρησαν, ότι η υπηρεσία DOGE της διοίκησης Τραμπ, ακυρώνοντας ένα κυβερνητικό συμβόλαιο, είχε εξοικονομήσει μόνο 8 εκατομμύρια δολάρια, αντί για τα 8 δισεκατομμύρια που είχε δηλώσει δημοσίως, το οποίο αποτελεί τεράστιο λάθος. Ένας αξιωματούχος είχε προφανώς διαβάσει λάθος το «8.000.000,00 δολάρια» ως «8.000.000.000 δολάρια».
Οδηγός για δημοσιογράφους που θέλουν να αποκτήσουν δωρεάν, ποιοτικές δορυφορικές εικόνες από οπουδήποτε στη Γη

Οι δημοσιογράφοι μπορούν πλέον να αποκτήσουν δωρεάν δορυφορικές εικόνες υψηλής ανάλυσης από όλο τον κόσμο σε λίγα λεπτά, χωρίς εξειδικευμένες γνώσεις.
Αναρωτηθείτε: «Τι έχω ξεχάσει;» Σε μια κωμική περίπτωση του 2021, το NPR (Νational Public Radio) έκανε αναφορά σε ένα τραγούδι του Broadway με έναν πολύ διάσημο αριθμητικό στίχο («Πεντακόσια είκοσι πέντε χιλιάδες εξακόσια λεπτά: πώς μετράς, πώς μετράς έναν χρόνο;»), σε έναν τίτλο που έγραφε «13.140.000 Λεπτά: Έχουν περάσει 25 χρόνια από την πρώτη παράσταση του: “Rent”». Αλλά αποδείχθηκε ότι το τραγούδι έθεσε ένα καλό ερώτημα και για τους δημοσιογράφους δεδομένων, επειδή οι συντάκτες της ιστορίας ξέχασαν να λάβουν υπόψη τις επτά επιπλέον ημέρες των ενδιάμεσων δίσεκτων ετών, οι οποίες είναι 527.040 λεπτά η καθεμία. Ως αποτέλεσμα, ο τίτλος έπρεπε να διορθωθεί και να αναφέρει «13.150.080 Λεπτά».
Διαβάστε το προσχέδιο δυνατά. Η μεγαλόφωνη ανάγνωση των θεμάτων δημοσιογραφίας δεδομένων έχει πολλά πλεονεκτήματα. «Πάντα διαβάζω δυνατά τα θέματά μου –είναι καλός τρόπος να καταλάβεις που έχεις υπερβολικά πολλά νούμερα», εξήγησε η Λα Φλερ. «Όταν κάνετε τις αναλύσεις σας, σιγουρευτείτε πως μπορείτε να τις εξηγήσετε σε λίγες προτάσεις. Το δοκίμαζα καλώντας τη μαμά μου και εξηγώντας το, και γρήγορα καταλάβαινα αν όντως “είχα” το θέμα μου». Η Ντάουελ συμφώνησε: «Το πιο σημαντικό είναι να αναδεικνύεις τα ευρήματά σου, χωρίς να κουράζεις το κοινό σου με μια σειρά από αριθμούς».
Oι ειδικές προτρέπουν τους δημοσιογράφους να «επιλέγουν τους αριθμούς τους με την ίδια προσοχή που επιλέγουν τα αποσπάσματα δηλώσεων» και να περιορίζουν τον συνολικό αριθμό των ψηφίων που παρουσιάζονται σε κάθε παράγραφο σε οκτώ.
Προσέξτε τους αριθμούς που ταιριάζουν στη δημοφιλή αφήγηση. Τον Φεβρουάριο, ένα σημαντικό θέμα δεδομένων στις ΗΠΑ κατέγραφε αρχικά το 14,5% ως ποσοστό θνησιμότητας από φωτιά για τα Tesla Cybertrucks. Αυτό αντιστοιχεί σε έναν θάνατο για κάθε επτά από αυτά τα πολιτικά πολωτικά οχήματα που κυκλοφορούν — ένα ανησυχητικά υψηλό ποσοστό που η κοινή λογική θα έπρεπε να θεωρήσει αμφισβητήσιμο. Η Λα Φλερ αναφέρθηκε στη μετέπειτα διόρθωση από το μέσο, που παραδέχτηκε ότι το πραγματικό ποσοστό ήταν 1.000 φορές χαμηλότερο, δηλαδή 14,5 θύματα ανά 100.000 οχήματα. (Επιπλέον, ακόμα και αυτός ο αριθμός ήταν λανθασμένος, λόγω του μικρού μεγέθους του δείγματος και της σύγκρισης μη συγκρίσιμων δεδομένων. Τα δεδομένα βασίζονταν σε μόνο δύο μόνο ατυχήματα, καθώς και στο περιστατικό με τον αυτοκτονικό βομβαρδισμό της Πρωτοχρονιάς στο Λας Βέγκας, ενώ υποτιμήθηκε ο αριθμός των αμφιλεγόμενων οχημάτων που πουλήθηκαν.)
Πάνω από όλα, «αν κάτι δεν σας φαίνεται σωστό, εμπιστευτείτε το ένστικτό σας», συμβούλευσε η Λα Φλερ.
Η Ντάουελ συνόψισε τις συμβουλές της με αυτόν τον τρόπο: «Θέστε ερωτήματα στις ιστορίες σας σχετικά με τη δική σας υπόθεση. Ίσως δεν είναι το θέμα που περιμένατε. Τα περισσότερα θέματα που γράφω δεν επιβεβαιώνουν ποτέ την αρχική μου θεωρία και καταλήγουμε να αλλάζουμε πορεία, το οποίο οδηγεί συχνά σε μια πιο ενδιαφέρουσα και πιο σωστή ιστορία».
Οι δύο ειδικές σε θέματα δεδομένων πρότειναν, επίσης, το φρεσκάρισμα των μαθηματικών γνώσεων και τις συμβουλές που περιλαμβάνονται στη δεύτερη έκδοση του οδηγού «Numbers in the Newsroom» του IRE, που γράφτηκε από τη Σάρα Κοέν (Sarah Cohen). Οι συμβουλές από αυτόν τον οδηγό περιλαμβάνουν τα εξής:
Προσπαθήστε να κρατήσετε τον συνολικό αριθμό των ψηφίων σε μία παράγραφο σε οκτώ ή λιγότερα. Ως κατευθυντήρια γραμμή —όχι ως κανόνα—, οι ειδικές προτρέπουν τους δημοσιογράφους να «επιλέγουν τους αριθμούς τους με την ίδια προσοχή που επιλέγουν τα αποσπάσματα δηλώσεων» και να περιορίζουν τον συνολικό αριθμό των ψηφίων που παρουσιάζονται σε κάθε παράγραφο σε οκτώ. Αυτό συχνά μεταφράζεται σε αναφορά σε δύο ξεχωριστά νούμερα (όπως ποσοστά) και ένα έτος. Για παράδειγμα, η ακόλουθη πρόταση έχει λίγα παραπάνω ψηφία, αλλά θα πλησίαζε στην κατευθυντήρια γραμμή χωρίς τα δεκαδικά νούμερα: «Ο προϋπολογισμός του Γραφείου Πλεονασμού αυξήθηκε κατά 48% το 2024, από 700,3 εκατομμύρια δολάρια σε 1,03 δισεκατομμύρια δολάρια». [ΣτΜ: Τέτοιο γραφείο ή κυβερνητικός οργανισμός δε υπάρχει. Πρόκειται για χιουμοριστική ή σατιρική επινόηση, που συχνά χρησιμοποιείται στα αγγλικά, για να σχολιάσει κριτικά τη γραφειοκρατική αναποτελεσματικότητα, τη σπατάλη κρατικών πόρων ή τις υπερβολικά περίπλοκες διοικητικές δομές.] Ακόμα καλύτερα, θα μπορούσε να μειωθεί σε μόνο έναν αριθμητικό δείκτη: «Το περασμένο έτος, ο προϋπολογισμός του Γραφείου Πλεονασμού αυξήθηκε σχεδόν κατά το ήμισυ, φτάνοντας το ένα δισεκατομμύριο δολάρια».
Αποφύγετε τον μέσο όρο των μέσων όρων. Η Κοέν συγκρίνει αυτό το κοινό λάθος στον δημοσιογραφικό χώρο με το «να παραβράζετε μια ποικιλία λαχανικών» και γράφει: «Μερικές φορές, οι δημοσιογράφοι παίρνουν μια σειρά από ποσοστιαίες αλλαγές, ας πούμε, σε έναν προϋπολογισμό, και υπολογίζουν έναν μέσο όρο για τη “μέση ποσοστιαία αλλαγή”. Αυτό αντιμετωπίζει το ίδιο την αύξηση κατά 140% σε ένα νέο, μικρό τμήμα με την αύξηση κατά 2% για την εκπαίδευση».
Χρησιμοποιήστε μια απλή μέθοδο, για να υπολογίσετε τις πιθανότητες κινδύνου «ένα από». Ο υπολογισμός και η αναφορά της πιθανότητας σπάνιων γεγονότων φαίνονται πολύπλοκοι, αλλά στην πραγματικότητα δεν είναι. Αν, κάθε χρόνο, 20 άτομα σε μια πόλη των 4,3 εκατομμυρίων πλήττονται από κεραυνό, η διαίρεση αυτών των θυμάτων με τον πληθυσμό θα φέρει ως αποτέλεσμα έναν αριθμό που φαίνεται άσχετος, το 0,000005. Αλλά η Κοέν σημειώνει ότι μπορείτε απλά να διαιρέσετε το νούμερο ένα με αυτά τα μικρά ποσά για να βρείτε το λογικό «ένα από» — στην προκειμένη περίπτωση, οι πιθανότητες να χτυπηθεί κάποιος από κεραυνό σε αυτήν την πόλη, στη διάρκεια ενός χρόνου, είναι μία στις 200.000.

