Ένα γλωσσάρι βασικών όρων για αρχάριους στην ανάλυση δεδομένων και για όσους έχουν απορίες γύρω από στατιστικές έννοιες που εκφέρονται στον δημόσιο λόγο.
- ακραία τιμή
- ανεξάρτητη μεταβλητή
- απογραφή
- διακριτή μεταβλητή
- διακύμανση
- διάμεσος
- δείγμα
- δειγματοληψία
- επαγωγική στατιστική
- επικρατούσα τιμή
- εύρος
- z-score
- κανονικοποίηση
- κατηγορική μεταβλητή
- κλίμακα
- κυλιόμενος μέσος όρος
- Likert scale
- μέση τιμή
- μεταβλητή
- μεταβολή
- n
- Ν
- ονομαστική μεταβλητή
- παρατήρηση
- περιγραφική στατιστική
- πληθυσμός
- ποιοτική μεταβλητή
- ποσοστιαία μεταβολή
- ποσοστιαία μονάδα
- ποσοτική μεταβλητή
- ρυθμός ανάπτυξης/μεταβολής
- συνεχής μεταβλητή
- συσχέτιση
- τιμή
- τυπική απόκλιση
- τυπική τιμή
- υπόθεση έρευνας
Α
ακραία τιμή (outlier)
μελετώντας μόνο μία μεταβλητή/διάσταση, «ακραία» τιμή (outlier) είναι εκείνη που βρίσκεται στα άκρα μιας στατιστικής κατανομής, δηλαδή είναι πολύ μικρότερη ή πολύ μεγαλύτερη από τις υπόλοιπες τιμές του υπό μελέτη συνόλου. Έτσι, δύναται να επηρεάσει σημαντικά, και πιθανώς εσφαλμένα, τον μέσο όρο, γι’ αυτό και συχνά εξαιρείται κατά τον υπολογισμό του. Σε άλλες περιπτώσεις, ακραίες τιμές μπορεί να υποδηλώνουν δεδομένα που προέρχονται από διαφορετικό πληθυσμό από εκείνο των υπόλοιπων παρατηρήσεων.
ανεξάρτητη μεταβλητή (independent variable)
όρος ευρείας χρήσης που διακρίνει τις μεταβλητές κατά τη μελέτη της επίδρασης μιας μεταβλητής (ανεξάρτητη) σε μια άλλη (εξαρτημένη). Σε γενικές γραμμές, θα μπορούσε να περιγραφεί ως η μεταβλητή που δεν επηρεάζεται, αλλά δύναται να επηρεάσει μια άλλη. Βοηθά κανείς να έχει στο μυαλό του ότι, στη σχέση αιτίου-αιτιατού, η ανεξάρτητη μεταβλητή θα αντιπροσώπευε το αίτιο. Για παράδειγμα, αν μελετούσαμε την πιθανή σχέση εξάρτησης μεταξύ κατά κεφαλήν ΑΕΠ και προσδόκιμου ζωής, το πρώτο θα ήταν η ανεξάρτητη μεταβλητή. Εάν το ερευνητικό ερώτημά μας ήταν αν το ύψος του κατώτατου μισθού επηρεάζει το ποσοστό ανεργίας, ο κατώτατος μισθός θα ήταν η ανεξάρτητη μεταβλητή. Στην επιστημονική πειραματική έρευνα, την ανεξάρτητη μεταβλητή χειρίζεται ο ερευνητής, ώστε να μετρήσει την επίδρασή της στην εξεταζόμενη εξαρτημένη μεταβλητή. Για παράδειγμα, η ουσία που λαμβάνουν συμμετέχοντες σε κλινική δοκιμή (φάρμακο/εμβόλιο ή placebo) είναι η ανεξάρτητη μεταβλητή, το αποτέλεσμά της είναι η εξαρτημένη μεταβλητή. Η διάκριση των μεταβλητών σε ανεξάρτητες και εξαρτημένες διαδραματίζει κεντρικό ρόλο και σε άλλα ερευνητικά πεδία, όπως η μηχανική μάθηση και η δημιουργία μοντέλων πρόβλεψης.
απογραφή (census)
έρευνα κατά την οποία συλλέγονται στοιχεία για όλες τις μεμονωμένες μονάδες ενός πληθυσμού. Για παράδειγμα, κατά την Απογραφή Θεραπευτηρίων 2019 από την Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ), συλλέχθηκαν στοιχεία από όλα τα νοσοκομεία και τις κλινικές της Ελλάδας. Το πιο κοινό παράδειγμα απογραφικής έρευνας είναι η απογραφή του πληθυσμού μιας χώρας.
B
Γ
Δ
διακριτή μεταβλητή (discrete variable)
ποσοτική μεταβλητή που μπορεί να πάρει συγκεκριμένες τιμές. Συνήθως, οι τιμές της είναι ακέραιοι αριθμοί –ας πούμε, ο αριθμός κλινών ενός νοσοκομείου: μπορεί να είναι 30, 50, 60, 100 κ.ο.κ.. Οι διακριτές μεταβλητές ονομάζονται και ασυνεχείς. Στον αντίποδα, βρίσκονται οι συνεχείς μεταβλητές, δηλαδή οι ποσοτικές μεταβλητές που μπορούν να πάρουν αμέτρητες τιμές (π.χ. 1,80, 1,805, 1,809595959 κλπ).
διακύμανση (variance)
ένα από τα μέτρα διασποράς (ή μέτρα μεταβλητότητας), που διαδραματίζει κεντρικό ρόλο στη στατιστική. Δηλώνει την απόκλιση των τιμών μιας μεταβλητής από την «κεντρική» θέση –δηλαδή, μετρά πόσο μακριά εκτείνεται ένα σύνολο αριθμών από τη μέση τιμή του υπό μελέτη συνόλου. Μαθηματικά, εκφράζεται ως ο μέσος όρος των τετραγώνων των αποκλίσεων των τιμών από τον μέσο όρο τους. Το μειονέκτημα, λοιπόν, είναι ότι η διακύμανση εκφράζεται με το τετράγωνο της εκάστοτε μονάδας μέτρησης –και όχι με τη μονάδα μέτρησης στην οποία εκφράζονται τα ίδια τα στατιστικά δεδομένα.
Για παράδειγμα, έστω ότι έχουμε δύο σύνολα αριθμών, που δηλώνουν μέτρα, ως εξής:
Σύνολο Α’ = 1 + 2 + 3 + 4 + 5 μ.
Σύνολο Β’ = 0 + 1 + 2 + 5 + 7 μ.
Και στις δύο περιπτώσεις, ο μέσος όρος του συνόλου είναι 3. Όμως, υπολογίζοντας τη διακύμανση σε κάθε σύνολο, τα πράγματα αλλάζουν.
Σύνολο Α’ – Διακύμανση:
( (1-3)2 + (2-3)2 + (3-3)2 + (4-3)2 + (5-3)2 ) / 5 =
(4 + 1 + 0 + 1 + 4) / 5 = 2 τ.μ.
Σύνολο Β’ – Διακύμανση:
( (0-3)2 + (1-3)2 + (2-3)2 + (5-3)2 + (7-3)2 ) / 5 =
(9 + 4 + 1 + 4 + 16) / 5 = 6,8 τ.μ.
Σε αυτό το παράδειγμα, η διακύμανση εκφράζεται σε τετραγωνικά μέτρα (τ.μ.). Στο Σύνολο Β’, η διακύμανση είναι μεγαλύτερη. Άρα, υπάρχει μεγαλύτερη διασπορά τιμών (ετερογένεια), σε σχέση με το Σύνολο Α’, όπου υπάρχει μεγαλύτερη «συσπείρωση» τιμών γύρω από την «κεντρική» θέση.
διάμεσος (median)
η μεσαία τιμή ενός συνόλου τιμών, διατεταγμένων σε αύξουσα σειρά. Για παράδειγμα, έστω ότι έχουμε τους μισθούς επτά υπαλλήλων ως εξής:
700, 800, 800, 950, 1.200, 1.500, 2.000
Ο αριθμός 950 είναι εκείνος που έχει στα αριστερά του όσες τιμές έχει και στα δεξιά του (από τρεις). Επομένως, ο διάμεσος μισθός των εν λόγω υπαλλήλων είναι 950 ευρώ.
Σε περίπτωση που το πλήθος των παρατηρήσεων είναι άρτιο (ζυγός αριθμός), τότε η διάμεσος είναι ο μέσος όρος των δύο μεσαίων τιμών. Στο παραπάνω παράδειγμα, ενώ η διάμεσος ισούται με 950, ο μέσος όρος της μισθοδοσίας είναι 1.136 ευρώ (άθροισμα μισθών/ πλήθος υπαλλήλων). Αυτό συμβαίνει, επειδή ο μέσος όρος επηρεάζεται από τις ακραίες τιμές του δείγματος. Γι’ αυτό και η διάμεσος συχνά προτιμάται στις αναλύσεις έναντι του μέσου όρου.
δείγμα (sample)
υποσύνολο ενός πληθυσμού –δηλαδή, δεδομένα τα οποία συλλέγονται από τον πληθυσμό, προκειμένου η ανάλυσή τους να οδηγήσει σε ασφαλώς γενικεύσιμα συμπεράσματα για το σύνολο (πληθυσμός). Το μέγεθος του στατιστικού δείγματος συνήθως συμβολίζεται με το λατινικό γράμμα n. Για παράδειγμα, σε έρευνα για την τηλεργασία ιδιωτικών υπαλλήλων, με τη συμμετοχή 2.000 ερωτώμενων εργαζομένων, στην ταυτότητα της μελέτης θα μπορούσε να αναφέρεται n=2.000. Τότε, ο πληθυσμός, που συνήθως συμβολίζεται ως Ν, θα ήταν το σύνολο των ιδιωτικών υπαλλήλων στη χώρα.
δειγματοληψία (sampling)
η τεχνική επιλογής του στατιστικού δείγματος. Η τυχαία δειγματοληψία (δείγματα πιθανότητας) είναι η κατάλληλη για την εμπειρική έρευνα, επειδή επιτρέπει την αντιπροσώπευση του πληθυσμού και τη γενίκευση των συμπερασμάτων –από το δείγμα στον πληθυσμό. Απλή τυχαία, στρωματοποιημένη, συστηματική και κατά συστάδες είναι τα τέσσερα είδη της τυχαίας δειγματοληψίας. Στον αντίποδα, η μη τυχαία δειγματοληψία (δείγματα μη-πιθανότητας) βασίζεται σε κριτήρια όπως η ευκολία, η διαθεσιμότητα, η ταχύτητα της συλλογής των δεδομένων κ.α., αλλά δεν μας επιτρέπει να γενικεύσουμε τα αποτελέσματα στον πληθυσμό.
E
επαγωγική στατιστική (inferential statistics)
αποκαλούμενη και στατιστική συμπερασματολογία, είναι ο κλάδος της στατιστικής που μελετά τα χαρακτηριστικά και αναλύει τα δεδομένα ενός υποσυνόλου (βλ. δείγμα), με στόχο την εξαγωγή αντίστοιχων συμπερασμάτων για το σύνολο (βλ. πληθυσμός). Πρόκειται, δηλαδή, για τη στατιστική που κάνει επαγωγή από το δείγμα στον πληθυσμό. Εδώ, γίνεται κατανοητό πόσο σημαντικές είναι η δειγματοληψία και η μεθοδολογία της ανάλυσης πριν από την εξαγωγή συμπερασμάτων.
επικρατούσα τιμή (mode)
η παρατήρηση με τη μεγαλύτερη συχνότητα, δηλαδή η τιμή που συναντάται περισσότερες φορές σε ένα σύνολο τιμών. Έστω ότι έχουμε το παράδειγμα της μηνιαίας μισθοδοσίας επτά υπαλλήλων, που χρησιμοποιήθηκε και παραπάνω (βλ. διάμεσος):
700, 800, 800, 950, 1.200, 1.500, 2.000
Εδώ, η επικρατούσα τιμή είναι τα 800 ευρώ. Η διάμεσος είναι τα 950 ευρώ και ο μέσος όρος είναι τα περίπου 1.136 ευρώ. Αναλύοντας τη μισθοδοσία του παραδείγματος, κανείς θα μπορούσε να πει ότι, ναι, μεν η διάμεση αμοιβή είναι 950 ευρώ, αλλά η συνηθέστερη είναι 150 ευρώ χαμηλότερη. Ο δε μέσος όρος της μισθοδοσίας, στην πραγματικότητα, διαμορφώνεται από έναν συγκριτικά υψηλόμισθο υπάλληλο.
εύρος (range)
η διαφορά της ελάχιστης τιμής από τη μέγιστη –πρόκειται για το απλούστερο από τα μέτρα διασποράς. Στο παράδειγμα της μισθοδοσίας, το εύρος είναι 1.300 ευρώ (2.000 – 700).
Z
z-score
η τυπική τιμή (standardized value) ή z-τιμή δηλώνει την απόσταση μιας παρατήρησης από τον μέσο όρο. Μαθηματικά, εκφράζεται ως το πηλίκο της εξής διαίρεσης: η διαφορά μιας τιμής από τον μέσο όρο προς την τυπική απόκλιση –z = (x – μ) / σ, όπου μ ο μέσος όρος και σ η τυπική απόκλιση. Όταν το z-score είναι θετικό, σημαίνει ότι η αρχική τιμή είναι μεγαλύτερη του μέσου όρου –και αντιθέτως, όταν το z-score έχει αρνητικό πρόσημο. Επειδή οι τυπικές τιμές εκφράζονται σε μονάδες τυπικής απόκλισης, είναι ανεξάρτητες από την αρχική μονάδα μέτρησης. Έτσι, προσφέρουν τη δυνατότητα σύγκρισης τιμών που προέρχονται από διαφορετικές κατανομές. Δείτε πώς εξηγεί το z-score η πλατφόρμα EuroMOMO και πώς το χρησιμοποιεί για τη σύγκριση της θνησιμότητας σε διαφορετικές ευρωπαϊκές χώρες και σε διαφορετικές χρονικές περιόδους.
Η
Θ
Ι
Κ
κανονικοποίηση (normalization)
μπορεί να σημαίνει πολλά πράγματα σε εφαρμογές της στατιστικής. Στην απλούστερη και συνηθέστερη περίπτωση, η κανονικοποίηση των αριθμών σημαίνει την προσαρμογή τιμών διαφορετικής κλίμακας σε μια κοινή κλίμακα, προκειμένου να είναι συγκρίσιμες. Για παράδειγμα, όλες οι έρευνες που αναφέρονται σε «ανά 100 χιλιάδες κατοίκους» μιλούν για κανονικοποιημένους αριθμούς. Τον τελευταίο χρόνο, το πιο κοινό παράδειγμα είναι τα κρούσματα COVID-19, οι αριθμοί των οποίων κανονικοποιούνται ανά 100 χιλιάδες ή ανά 1 εκατομμύριο κατοίκους –ιδίως σε αναλύσεις όπου συγκρίνονται διαφορετικές, πληθυσμιακά, χώρες ή περιοχές. Εάν δεν συνέβαινε αυτό, στους αριθμούς των κρουσμάτων, εν πολλοίς θα «καθρεφτιζόταν» ο πληθυσμός των χωρών.
Στον παραπάνω παγκόσμιο χάρτη κρουσμάτων από την αρχή της πανδημίας, οι χώρες «χρωματίζονται» με βάση τα κανονικοποιημένα κρούσματα ανά 100 χιλιάδες κατοίκων τοπικού πληθυσμού. Έτσι, επιτρέπεται να διαπιστώσουμε ότι, για παράδειγμα, η Σουηδία έχει βρεθεί σχεδόν στην ίδια θέση με τις ΗΠΑ.
κατηγορική μεταβλητή (categorical variable)
ποιοτική μεταβλητή οι τιμές της οποίας μπορεί να είναι χαρακτηριστικά γνωρίσματα άνευ κατάταξης ή περιλαμβανομένης: οι κατηγορικές μεταβλητές διακρίνονται σε ονομαστικές (nominal) και τακτικές (ordinal). Όσον αφορά στις ονομαστικές μεταβλητές, πρόκειται για ποιοτικά χαρακτηριστικά σε καλά προσδιορισμένες, διακριτές, αμοιβαία αποκλειόμενες και ισοδύναμες κατηγορίες. Τα πιο κοινά παραδείγματα ονομαστικών μεταβλητών είναι η εθνικότητα, η οικογενειακή κατάσταση, το θρήσκευμα κλπ. Τακτική μεταβλητή είναι εκείνη σε κατάταξη (διέπεται από διαβάθμιση). Για παράδειγμα, ο βαθμός ικανοποίησης από το κυβερνητικό έργο («καθόλου», «λίγο», «μέτρια», «πολύ», «απολύτως») είναι τακτική ποιοτική μεταβλητή.
κλίμακα (scale)
κατηγοριοποίηση της μέτρησης σε τέσσερα είδη: ονομαστική, τακτική, διαστημική/αριθμητική και αναλογική κλίμακα
κυλιόμενος μέσος όρος (moving/rolling average)
πολύ συχνά χρησιμοποιείται σε δεδομένα χρονοσειράς (time series data), προκειμένου να εξομαλύνει τις βραχυπρόθεσμες διακυμάνσεις (όπως, για παράδειγμα, προβλήματα στις καταγραφές) και να αναδείξει ορθότερα πιο μακροπρόθεσμες τάσεις.
Για παράδειγμα, στο παραπάνω διάγραμμα, στο οποίο απεικονίζεται η εξέλιξη των ημερήσιων κρουσμάτων COVID-19 στην Ελλάδα στον χρόνο, η γραμμή με το σκούρο μπλε χρώμα δηλώνει τον κυλιόμενο μέσο όρο 7 ημερών: σχηματίζεται, καταγράφοντας, για κάθε ημέρα, τον μέσο όρο των ημερήσιων κρουσμάτων, με βάση τα δεδομένα των τελευταίων επτά ημερών κάθε φορά. Κατ’ αυτόν τον τρόπο, εξομαλύνονται οι τιμές των ημερήσιων καταγεγραμμένων κρουσμάτων (γαλάζιες μπάρες), οι οποίες δύνανται να επηρεάζονται από καταγραφικά προβλήματα, τον αντίστοιχο ημερήσιο αριθμό διεξαχθέντων τεστ κ.α..
Λ
Likert scale (κλίμακα Likert)
ψυχομετρική τακτική κλίμακα μέτρησης, που αρχικά δημιουργήθηκε από τον Αμερικανό ψυχολόγο, Ρένσις Λίκερτ, από τον οποίο πήρε και το όνομά της. Η πενταβάθμια κλίμακα Likert χρησιμοποιείται ευρέως στην κοινωνική έρευνα. Κάθε φορά που απαντάμε σε ερωτηματολόγια «κλειστού τύπου», επιλέγοντας «Διαφωνώ απολύτως» ή «Διαφωνώ» ή «Ούτε συμφωνώ ούτε διαφωνώ» ή «Συμφωνώ» ή «Συμφωνώ απολύτως», κατηγοριοποιούμε την προτίμησή μας με βάση την κλίμακα Likert.
M
μέση τιμή (mean)
o μέσος όρος ενός συνόλου n παρατηρήσεων –υπολογίζεται διαιρώντας το άθροισμα των παρατηρήσεων με το πλήθος τους. Δύναται να επηρεάζεται «εσφαλμένα», δηλαδή να μην αντικατοπτρίζει με ρεαλισμό μια κατάσταση, όταν ο υπολογισμός του επηρεάζεται από τυχόν ακραίες τιμές που υπάρχουν στο δείγμα. Τότε, ο μέσος όρος μπορεί να υποτιμά ή να υπερτιμά μια κατάσταση, γι’ αυτό και συνίσταται η σύγκρισή του με τη διάμεσο, η οποία και προτιμάται στην ανάλυση, ιδίως όταν εντοπίζεται μεγάλη διαφορά μεταξύ των δύο.
μεταβλητή (variable)
το χαρακτηριστικό ως προς το οποίο εξετάζουμε τον μελετώμενο πληθυσμό. Για παράδειγμα, μερικές μεταβλητές που μελετάμε καθημερινά σε αναλύσεις για την πανδημία: χώρα, ημερήσια κρούσματα, ημερήσιοι θάνατοι, διασωληνωμένοι ασθενείς, νέα διεξαχθέντα τεστ, ημερήσιες δόσεις εμβολίου κ.ο.κ..
μεταβολή (change)
η αλλαγή της τιμής ή των τιμών μιας μεταβλητής –συνήθως, σε μια χρονική στιγμή σε σχέση με μία άλλη, συγκρίσιμη, στιγμή. Για παράδειγμα, σύμφωνα με πρόσφατη έρευνα της ΕΛΣΤΑΤ για την οικοδομική δραστηριότητα στην Ελλάδα, τον Ιανουάριο 2021 (προσωρινά στοιχεία), στην Αττική εκδόθηκαν 353 οικοδομικές άδειες: δηλαδή, 79 περισσότερες σε σύγκριση με τον Ιανουάριο 2020, οπότε είχαν εκδοθεί 274 άδειες. Τις περισσότερες φορές, η μεταβολή εκφράζεται ως ποσοστό (βλ. ποσοστιαία μεταβολή). Ειδάλλως, σε περίπτωση που εκφράζεται σε απόλυτους αριθμούς, πρόκειται μόνο για διαφορά, εφόσον η αρχική τιμή απλώς αφαιρείται από την τελευταία.
N
n
λατινικός χαρακτήρας με τον οποίο συνήθως συμβολίζεται το μέγεθος του δείγματος. Για παράδειγμα, όταν το iMEdD Lab δημοσίευσε τη γεωγραφική κατανομή των θανάτων από COVID-19 στην Ελλάδα, τον Δεκέμβριο 2020, με βάση δείγμα 3.214 απωλειών (σε σύνολο 3.687 ως τις 14 Δεκεμβρίου), θα μπορούσε να αναφέρεται: n = 3.214.
Ν
λατινικός χαρακτήρας με τον οποίο συνήθως συμβολίζεται το μέγεθος του πληθυσμού –σε αντιπαραβολή με το n, που συνήθως δηλώνει το μέγεθος του δείγματος. Για παράδειγμα, όταν το iMEdD Lab δημοσίευσε τη γεωγραφική κατανομή των θανάτων από COVID-19 στην Ελλάδα, τον Δεκέμβριο 2020, με βάση δείγμα 3.214 απωλειών (σε σύνολο 3.687 ως τις 14 Δεκεμβρίου), θα μπορούσε να αναφέρεται: n = 3.214, Ν = 3.687.
Ξ
Ο
ονομαστική μεταβλητή (nominal variable)
πρόκειται για ποιοτικά χαρακτηριστικά (κατηγορικές μεταβλητές), τα οποία εντάσσονται σε καλά προσδιορισμένες, διακριτές, αμοιβαία αποκλειόμενες και ισοδύναμες κατηγορίες, που δεν διέπονται από κατάταξη. Τα πιο κοινά παραδείγματα ονομαστικών μεταβλητών είναι η εθνικότητα, η οικογενειακή κατάσταση, το θρήσκευμα κλπ.
Π
παρατήρηση (observation)
η τιμή που παίρνει μια μεταβλητή, ως μέρος μιας σειράς δεδομένων που έχουν συλλεχθεί από επιλεγμένες μονάδες του πληθυσμού (δείγμα). Οι παρατηρήσεις (ή, αλλιώς, τα στατιστικά δεδομένα) μπορεί να είναι ποιοτικές ή αριθμητικές. Σε μια σειρά δεδομένων, οι παρατηρήσεις δεν είναι απαραίτητα διαφορετικές. Για παράδειγμα, αν ρωτήσουμε δέκα ανθρώπους ποιο κόμμα ψηφίζουν, έχουμε δέκα παρατηρήσεις. Από αυτές, οι τέσσερις μπορεί να είναι κοινές, εάν τέσσερις ερωτώμενοι δηλώσουν ότι ψηφίζουν το ίδιο κόμμα. Ή, εάν ρωτήσουμε πέντε ανθρώπους στην Αθήνα από ποια περιφέρεια της Ελλάδας κατάγονται, καθένας τους δύναται να απαντήσει μία διαφορετική από τις 13 περιφέρειες της χώρας. Στην πραγματικότητα, μπορεί να πάρουμε απαντήσεις (δηλαδή, να συλλέξουμε παρατηρήσεις) όπως:
Κεντρική Μακεδονία, Κεντρική Μακεδονία, Αττική, Κρήτη, Θεσσαλία, Αττική
περιγραφική στατιστική (descriptive statistics)
o κλάδος της στατιστικής που ασχολείται με την περιγραφή των δεδομένων, δηλαδή με τη συνοπτική και αποτελεσματική παρουσίασή τους. Για παράδειγμα, εάν εξετάζοντας ένα δείγμα 100 αποφοίτων ενός πανεπιστημιακού τμήματος, αναφέρουμε ότι 40 στους 100 αποφοίτησαν με «Άριστα», τότε περιγράφουμε αυτό που παρατηρήσαμε. Εάν αναφέρουμε ότι το 40% των φοιτητών του τμήματος αποφοιτά με «Άριστα», τότε προβαίνουμε σε στατιστική συμπερασματολογία (βλ. επαγωγική στατιστική). Στην τελευταία περίπτωση, γίνεται κατανοητό πόσο σημαντική είναι η επιλογή του δείγματος (βλ. δειγματοληψία).
πληθυσμός (population)
ένα σύνολο το οποίο εξετάζεται ως προς ένα ή περισσότερα χαρακτηριστικά του –συνήθως, μέσα από την ανάλυση ενός δείγματος, εκτός εάν πρόκειται περί απογραφής. Για παράδειγμα, εάν θέλουμε να εξετάσουμε την πρόθεση ψήφου ενόψει εκλογών, ο πληθυσμός είναι το σύνολο των ατόμων που έχουν δικαίωμα ψήφου στις επερχόμενες εκλογές. Συνήθως συμβολίζεται με τον λατινικό χαρακτήρα N. Τα στοιχεία του πληθυσμού μερικές φορές αναφέρονται ως μονάδες.
ποιοτική μεταβλητή (qualitative variable)
οι τιμές της οποίας δεν είναι αριθμοί. Για παράδειγμα, το φύλο, το θρήσκευμα, το επίπεδο εκπαίδευσης, η πολιτική τοποθέτηση, η οικογενειακή κατάσταση είναι ποιοτικές μεταβλητές –διακρίνονται σε ονομαστικές και σε τακτικές. Για παράδειγμα, η οικογενειακή κατάσταση είναι ονομαστική ποιοτική μεταβλητή, ενώ ο βαθμός ικανοποίησης από το κυβερνητικό έργο («καθόλου», «λίγο», «μέτρια», «πολύ», «απολύτως») είναι τακτική ποιοτική μεταβλητή.
ποσοστιαία μεταβολή (percentage change)
η σχετική διαφορά δύο αριθμών από μια χρονική στιγμή σε μια άλλη. Υπολογίζεται με τον τύπο:
( (V2 – V1) / V1 ) * 100,
όπου V2, η πιο πρόσφατη τιμή και V1, η αρχική τιμή. Για παράδειγμα, σύμφωνα με πρόσφατη έρευνα της ΕΛΣΤΑΤ για την οικοδομική δραστηριότητα στην Ελλάδα, τον Ιανουάριο 2021 (προσωρινά στοιχεία), στην Αττική εκδόθηκαν 353 οικοδομικές άδειες, ενώ τον Ιανουάριο 2020 είχαν εκδοθεί 274 άδειες. Επομένως, η ποσοστιαία μεταβολή υπολογίζεται ως εξής:
( (353 – 274) / 274 ) * 100 = 28,8%
Αυτό σημαίνει ότι η έκδοση οικοδομικών αδειών παρουσίασε αύξηση κατά 28,8%, σε σχέση με την ίδια περίοδο την προηγούμενη χρονιά.
Αρνητική ποσοστιαία μεταβολή σημαίνει μείωση. Δηλαδή, αν το αποτέλεσμα του υπολογισμού ήταν -28,8%, τότε θα λέγαμε ότι παρουσιάζεται μείωση κατά 28,8%.
ποσοστιαία μονάδα (percentage point)
η αριθμητική διαφορά μεταξύ δύο ποσοστών. Για παράδειγμα, σε δημοσκόπηση για την πρόθεση ψήφου, αν ένα κόμμα συγκεντρώνει το 30% των απαντήσεων και ένα άλλο κόμμα συγκεντρώνει το 24% των απαντήσεων, τότε το πρώτο είναι «μπροστά» κατά 6 ποσοστιαίες μονάδες (και όχι «κατά 6%»).
ποσοτική μεταβλητή (quantitative variable)
οι τιμές της οποίας είναι αριθμοί. Οι ποσοτικές μεταβλητές διακρίνονται σε διακριτές ή ασυνεχείς και σε συνεχείς μεταβλητές.
Ρ
ρυθμός ανάπτυξης/μεταβολής (growth rate)
η μέση ποσοστιαία μεταβολή μιας τιμής στην πάροδο του χρόνου. Εάν υποθέσουμε ότι μελετάμε γραμμική ανάπτυξη, τότε ο ρυθμός ανάπτυξης/μεταβολής υπολογίζεται ως εξής:
( ( (V2 – V1) / t ) / V1 ) * 100,
όπου V2 η πιο πρόσφατη τιμή, V1 η αρχική τιμή και t, η χρονική διάρκεια.
Για παράδειγμα, σύμφωνα με τα ανοικτά δεδομένα της Παγκόσμιας Τράπεζας, το ετήσιο κατά κεφαλήν ΑΕΠ στην Ελλάδα διαμορφώθηκε, για τα έτη από το 2008 ως και το 2015, όπως φαίνεται στον παρακάτω πίνακα (σε δολάρια).
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 31997,28 | 29710,97 | 26917,76 | 25916,29 | 22242,68 | 21874,82 | 21760,98 | 18167,77 |
Εάν θέλαμε να υπολογίσουμε τον ετήσιο ρυθμό ανάπτυξης για αυτήν την επταετία, θα κάναμε το εξής:
( ( (18167,77 – 31997,28) / 7 ) / 31997,28 ) * 100 = -6,17%
Τότε, θα λέγαμε ότι ο ετήσιος ρυθμός ανάπτυξης για το κατά κεφαλήν ΑΕΠ στην Ελλάδα, από το 2008 ως το 2015, ήταν -6,17% –δηλαδή, ο ετήσιος ρυθμός ύφεσης ήταν 6,17%.
Σε blog του Πανεπιστημίου του Όρεγκον, έχουμε βρει μία από τις πιο κατανοητές εξηγήσεις για τη διαφορά μεταξύ ρυθμού μεταβολής και ποσοστιαίας μεταβολής.
Σ
συνεχής μεταβλητή (continuous variable)
ποσοτική μεταβλητή που μπορεί να πάρει αμέτρητες τιμές (π.χ. 1,80, 1,805, 1,809595959 κλπ). Στον αντίποδα, βρίσκονται οι διακριτές (ή ασυνεχείς) ποσοτικές μεταβλητές oι οποίες δύνανται να πάρουν συγκεκριμένες τιμές (συνήθως ακέραιοι αριθμοί) –για παράδειγμα, ο αριθμός κλινών ενός νοσοκομείου: μπορεί να είναι 30, 50, 60, 100 κ.ο.κ..
συσχέτιση (correlation)
ο όρος αναφέρεται σε ευρεία κατηγορία στατιστικών σχέσεων μεταξύ μεταβλητών, όπου, επίσης, δύναται να αναπτύσσεται σχέση εξάρτησης. Το πολύ σύνηθες είναι η «συσχέτιση» να χρησιμοποιείται για τον βαθμό κατά τον οποίο δύο μεταβλητές παρουσιάζουν γραμμική σχέση –δηλαδή, κατά πόσο είτε, όσο αυξάνεται η μία, αυξάνεται και η άλλη είτε, όσο μειώνεται η μία, μειώνεται και η άλλη είτε, όσο αυξάνεται η μία, μειώνεται η άλλη. Κοινής λήψης παράδειγμα είναι η συσχέτιση της τιμής ενός προϊόντος με τη ζήτηση που έχει. Υπάρχουν διάφοροι συντελεστές για τον υπολογισμό της συσχέτισης μεταξύ δύο μεταβλητών –ευρέως διαδεδομένος είναι ο επονομαζόμενος «συντελεστής συσχέτισης του Pearson» (Pearson’s correlation coefficient), ο οποίος έχει πάρει το όνομά του από τον εμπνευστή του, τον Άγγλο μαθηματικό Karl Pearson.
Ο συντελεστής συσχέτισης συνήθως συμβολίζεται με τον λατινικό χαρακτήρα r ή με το ρ και μπορεί να πάρει τιμές από -1 έως και 1:
-1 ≤ r ≤ 1
Όσο πιο κοντά στο 1 βρίσκεται ο συντελεστής συσχέτισης, τόσο πιο δυνατή θετική συσχέτιση υπάρχει. Αντιθέτως, όσο πιο κοντά στο -1 βρίσκεται το r, τόσο πιο δυνατή είναι η αρνητική συσχέτιση. Συντελεστής συσχέτισης ίσος με μηδέν (ή γύρω στο μηδέν) σημαίνει ότι δεν υπάρχει συσχέτιση μεταξύ των δύο μελετώμενων μεταβλητών. Χαρακτηριστική για την κατανόηση της συσχέτισης μεταξύ δύο μεταβλητών είναι η παρακάτω εικόνα από τη Wikipedia.
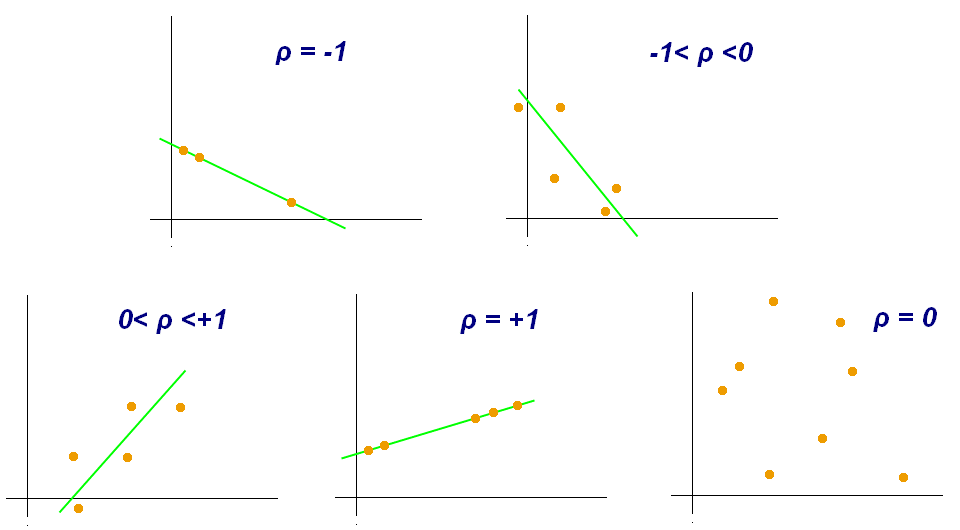
Μπορείτε να υπολογίσετε τη συσχέτιση μεταξύ δύο μελετώμενων μεταβλητών πολύ εύκολα, με τη χρήση λογιστικών φύλλων και της συνάρτησης =CORREL().
Επωδός όλων δικαίως αποτελεί η φράση «η συσχέτιση δεν σημαίνει αιτιότητα» («correlation does not imply causation»). Δηλαδή, το γεγονός ότι μια μεταβλητή αυξάνεται όσο αυξάνεται μια άλλη δεν σημαίνει απαραίτητα ότι η πρώτη αυξάνεται επειδή αυξάνεται η δεύτερη.
Τ
τιμή (value)
οι τιμές που δύναται να πάρει μια μεταβλητή λέγονται τιμές της μεταβλητής. Για παράδειγμα, έστω ότι ρωτάμε πέντε ανθρώπους στην Αθήνα από ποια περιφέρεια της Ελλάδας κατάγονται. Η μεταβλητή «περιφέρεια» δύναται να πάρει ως τιμή οποιαδήποτε από τις 13 περιφέρειες της χώρας. Οι απαντήσεις που θα λάβουμε από αυτούς τους πέντε ανθρώπους θα είναι οι παρατηρήσεις μας, δηλαδή τα στατιστικά δεδομένα. Σε μια σειρά δεδομένων, οι παρατηρήσεις δεν είναι απαραίτητα διαφορετικές. Στο παραπάνω παράδειγμα, οι τιμές που δύναται να πάρει η μεταβλητή είναι οι 13 περιφέρειες της χώρας, αλλά, στην πραγματικότητα, μπορεί να πάρουμε απαντήσεις (δηλαδή, να συλλέξουμε παρατηρήσεις) όπως:
Κεντρική Μακεδονία, Κεντρική Μακεδονία, Αττική, Κρήτη, Θεσσαλία, Αττική
τυπική απόκλιση (standard deviation)
ένα από μέτρα διασποράς (ή μέτρα μεταβλητότητας), με κεντρικό ρόλο στη στατιστική. Δηλώνει την απόκλιση των τιμών μιας μεταβλητής από την «κεντρική» θέση –δηλαδή, μετρά πόσο μακριά εκτείνεται ένα σύνολο αριθμών από τη μέση τιμή του υπό μελέτη συνόλου. Μαθηματικά, εκφράζεται ως η θετική τετραγωνική ρίζα της διακύμανσης (βλ. διακύμανση) και συνήθως συμβολίζεται με τον λατινικό χαρακτήρα s. Σε σχέση με τη διακύμανση, το πλεονέκτημα της τυπικής απόκλισης είναι ότι εκφράζεται με την ίδια μονάδα μέτρησης που εκφράζονται οι παρατηρήσεις. Για παράδειγμα, αν μελετάμε μια σειρά μισθολογικών δεδομένων σε ευρώ, η τυπική απόκλιση θα εκφράζεται, επίσης, σε ευρώ. Βοηθά κανείς να σκέφτεται ότι όσο μεγαλύτερη είναι η τυπική απόκλιση, τόσο μεγαλύτερη είναι η διασπορά των παρατηρήσεων –δηλαδή, τα δεδομένα μας δεν «συσπειρώνονται» αρκετά γύρω από τον μέσο όρο.
τυπική τιμή (z-score)
αλλιώς τιμή-z, δηλώνει την απόσταση μιας παρατήρησης από τον μέσο όρο. Μαθηματικά, εκφράζεται ως το πηλίκο της εξής διαίρεσης: η διαφορά μιας τιμής από τον μέσο όρο προς την τυπική απόκλιση –z = (x – μ) / σ, όπου μ ο μέσος όρος και σ η τυπική απόκλιση. Όταν το z-score είναι θετικό, σημαίνει ότι η αρχική τιμή είναι μεγαλύτερη του μέσου όρου –και αντιθέτως, όταν το z-score έχει αρνητικό πρόσημο. Επειδή οι τυπικές τιμές εκφράζονται σε μονάδες τυπικής απόκλισης, είναι ανεξάρτητες από την αρχική μονάδα μέτρησης. Έτσι, προσφέρουν τη δυνατότητα σύγκρισης τιμών που προέρχονται από διαφορετικές κατανομές. Δείτε πώς εξηγεί το z-score η πλατφόρμα EuroMOMO και πώς το χρησιμοποιεί για τη σύγκριση της θνησιμότητας σε διαφορετικές ευρωπαϊκές χώρες και σε διαφορετικές χρονικές περιόδους.
Υ
υπόθεση έρευνας (research hypothesis)
μια συγκεκριμένη, σαφής και ελέγξιμη δήλωση σχετικά με το πιθανό αποτέλεσμα μιας ερευνητικής μελέτης. Ο καθορισμός των ερευνητικών υποθέσεων είναι από τα σημαντικότερα βήματα κατά τον σχεδιασμό μιας ποσοτικής έρευνας. Οι εκ των προτέρων δηλωμένες, από την ερευνητική ομάδα, αυτές υποθέσεις συχνά καθορίζουν τον σχεδιασμό της μελέτης. Επιβεβαιώνονται ή διαψεύδονται κατόπιν στατιστικής ανάλυσης των δεδομένων.
Φ
Χ
Ψ
Ω
Η ανάλυση για την πορεία του Στέφανου Τσιτσιπά
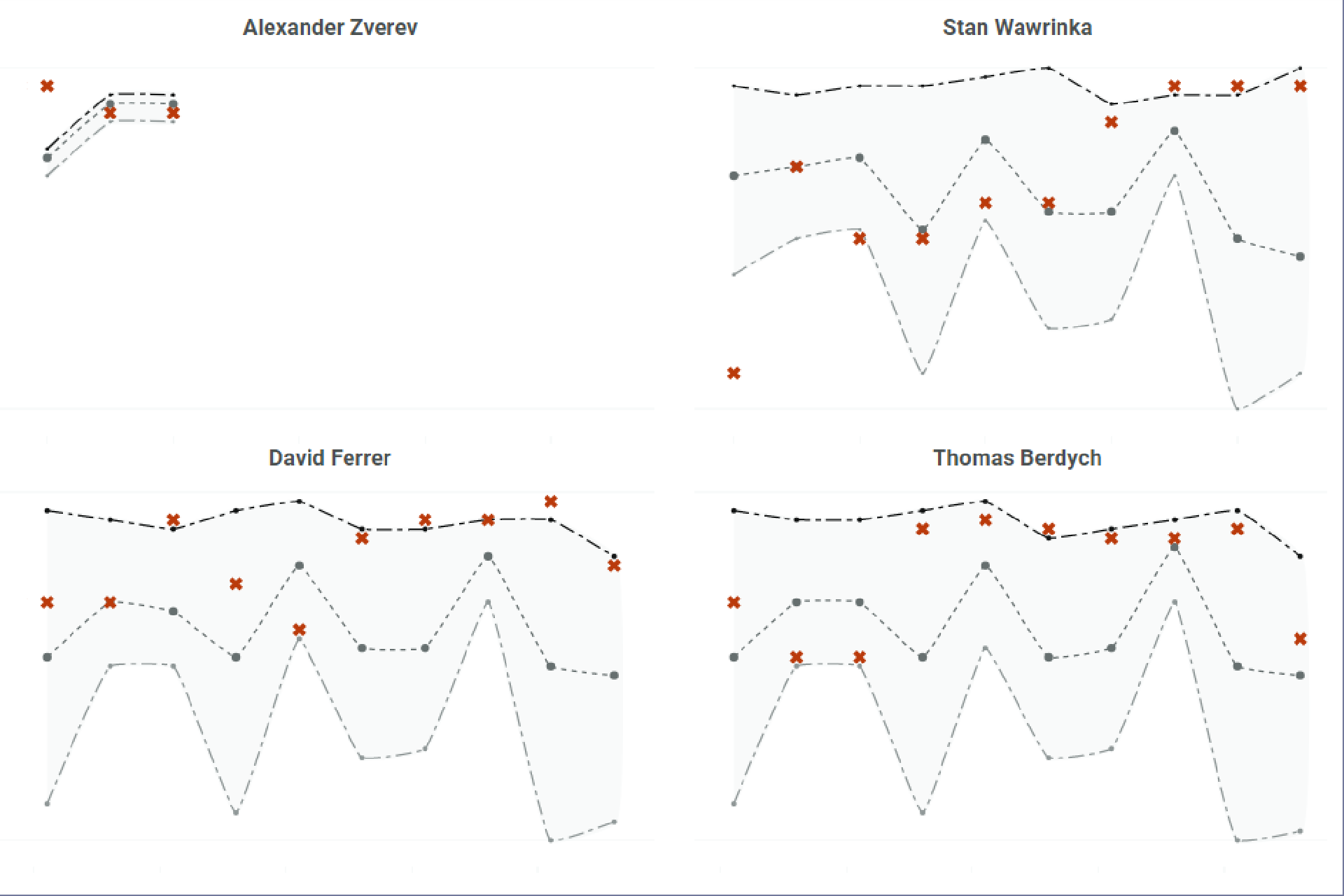
Πώς ομαδοποιήσαμε 1.602 αθλητές τένις, για να βρούμε με ποιους «μοιάζει» ο Στέφανος Τσιτσιπάς και να προβλέψουμε τη διαδρομή του.
Βιβλία που αξίζει να διαβάσετε
- Darrell Huff, How to Lie with Statistics, Penguin, Λονδίνο: 1991*
- Timothy C. Urdan, Statistics in Plain English, Routledge, Νέα Υόρκη: 2016
* Ή οποιαδήποτε έκδοση αυτού του θρυλικού βιβλίου που γράφτηκε από δημοσιογράφο-συγγραφέα το 1954 (βλ. Darrell Huff).
Χρήσιμοι σύνδεσμοι
- Ιουλία Παπαγεωργίου, Θεωρία Δειγματοληψίας, ΣΕΑΒ, ΕΜΠ: 2015, διαθέσιμο στο repository.kallipos.gr, άδεια χρήσης CC BY-NC-SA 3.0 GR
- Φωτόδεντρο – Διαδραστικά Σχολικά Βιβλία, Μαθηματικά και Στοιχεία Στατιστικής (Γ’ Λυκείου Γενικής Παιδείας) – Βιβλίο Μαθητή
- Eurostat, Statistics Explained
- OECD, Glossary of Statistical Terms
- Royal Statistical Society, Statistics for Journalists, Science and Statistics for Journalists Workshop, RSS & NCTJ, Bloomberg, Λονδίνο: 13 Νοεμβρίου 2014
Ευχαριστίες στον Δημήτρη Καρλή, Καθηγητή Στατιστικής στο Τμήμα Στατιστικής στο Οικονομικό Πανεπιστήμιο Αθηνών, για τις συμβουλές και τα σχόλιά του.