Πώς ομαδοποιήσαμε 1.602 διαφορετικούς αθλητές τένις, για να βρούμε με ποιους «μοιάζει» ο Στέφανος Τσιτσιπάς και να προβλέψουμε τη διαδρομή του κατά την επόμενη δεκαετία, με την εφαρμογή απλών τεχνικών μηχανικής μάθησης και στατιστικής.
Συλλογή δεδομένων
Τι λέει η στατιστική για την καριέρα του Στέφανου Τσιτσιπά

Με ποιους αθλητές μοιάζει ο 22χρονος διεθνής και πώς θα διαμορφωθεί η πορεία του την επόμενη δεκαετία.
Η συλλογή πρωτογενών στοιχείων έγινε τον Μάρτιο 2020 από την ιστοσελίδα Ultimate Tennis Statistics, η οποία φέρει Creative Commons άδεια χρήσης (CC BY-NC-SA 4.0) και βασίζεται σε ανοιχτά λογισμικά τα οποία είναι διαθέσιμα στο GitHub.
Συγκεκριμένα, συγκεντρώσαμε τα ετήσια δεδομένα, από το 2000 ως τον Μάρτιο 2020, για την κατάταξη των αθλητών σε παγκόσμιο επίπεδο, από τις σχετικές λίστες κατάταξης της Ένωσης Επαγγελματιών Αντισφαιριστών (Association of Tennis Professionals, ATP), όπως αυτές είναι δημοσιευμένες στην ιστοσελίδα Ultimate Tennis Statistics. Στη συνέχεια, αντλήσαμε δεδομένα προφίλ, τα οποία είναι δημοσιευμένα στην ίδια ιστοσελίδα, για 3.912 μοναδικούς αθλητές τένις που περιλαμβάνονται στις εν λόγω λίστες.
Ενδεικτικά, όπως φαίνεται από τη σελίδα για το προφίλ του Στέφανου Τσιτσιπά, τα εν λόγω «δεδομένα προφίλ» κάθε αθλητή, μεταξύ άλλων, περιλαμβάνουν πληροφορίες για την ηλικία του παίκτη, το έτος εκκίνησης επαγγελματικής σταδιοδρομίας, τις σεζόν δραστηριότητας, το «backhand» του, την αγαπημένη του αγωνιστική επιφάνεια, το ύψος των αμοιβών βραβείων που έχει εισπράξει, τους τίτλους τους οποίους έχει κερδίσει, τη διαχρονικά υψηλότερη και την ισχύουσα θέση του στην παγκόσμια κατάταξη, τη βαθμολογία του σε κλίμακα ELO κλπ.
Στόχος ήταν να κάνουμε εκτιμήσεις για την πορεία συγκεκριμένων παικτών –του Στέφανου Τσιτσιπά, με την αξιοποίηση δεδομένων για τη διαδρομή «όμοιων» αθλητών. Xρησιμοποιήσαμε τα διαθέσιμα στοιχεία, προκειμένου να δημιουργήσουμε ένα ενιαίο σύνολο δεδομένων (dataset), με σειρά μεταβλητών για κάθε παίκτη, τις οποίες θα μπορούσαμε να αναλύσουμε στατιστικά, ώστε να ομαδοποιήσουμε τους αθλητές, με βάση τον βαθμό ομοιότητάς τους, και να κάνουμε προβλέψεις για τη δυνητική διαδρομή τους.
Καθαρισμός δεδομένων
To σύνολο δεδομένων, που δημιουργήθηκε ως σύνθεση των παραπάνω στοιχείων, θα μπορούσε να περιγραφεί ως ένας πίνακας με n αριθμό γραμμών και p αριθμό στηλών: κάθε γραμμή αντιστοιχεί σε έναν αθλητή και κάθε στήλη αντιστοιχεί σε καθεμία από τις μεταβλητές προς ανάλυση, περιέχοντας τις ανάλογες τιμές.
Πριν να προβούμε σε οποιαδήποτε στατιστική ανάλυση, υπολογίσαμε πόσες ελλείπουσες παρατηρήσεις («missing values») αντιστοιχούν στις γραμμές και τις στήλες του dataset. Βρήκαμε ότι, σε αρκετές περιπτώσεις γραμμών και στηλών, οι κενές τιμές αναλογούσαν σε περισσότερο από το 50% των περιεχομένων τους. Επομένως, διαγράψαμε αυτές τις γραμμές και στήλες, που δεν θα μπορούσαν να παράσχουν παρά αμελητέα πληροφορία. Το αποτέλεσμα ήταν ένα τελικό σύνολο δεδομένων, με 1.602 γραμμές (παίκτες) και 20 μεταβλητές (ονόματα και χαρακτηριστικά παικτών).
Σε αυτό το dataset, οι υπόλοιπες ελλείπουσες τιμές (όσες διατηρήθηκαν μετά τη διαγραφή γραμμών και στηλών με κενές τιμές σε περισσότερο από το 50% των δεδομένων τους) συμπληρώθηκαν με την εφαρμογή τεχνικών στατιστικής μηχανικής μάθησης και με τη χρήση της στατιστικής γλώσσας προγραμματισμού R.
Δείγμα από το σύνολο δεδομένων προς ανάλυση
| names | prize_money | best_rank | overall_surface_pct | hard_surface_pct | clay_surface_pct | grass_surface_pct | ranksDiff1 | ranksDiff2 | ranksDiff3 | best_rank_std | age_turned_pro | age | plays | backhand | favorite_surface | hard_titles_std | clay_titles_std | titles_std | prize_money_std |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Feliciano Lopez | 777932.27 | 12 | 0.52 | 0.51 | 0.49 | 0.65 | 112.0 | 97.0 | 34.0 | 18.0 | 15.0 | 38.0 | 2 | 2 | 9 | 0.0909090909090909 | 0.0454545454545455 | 0.31818181818181795 | 13.5643947428156 |
| Nicolas Mahut | 513113.95 | 37 | 0.44 | 0.41 | 0.3 | 0.62 | 172.0 | 53.0 | 175.0 | 14.0 | 18.0 | 38.0 | 3 | 2 | 9 | 0.2 | 13.1482532242432 | ||
| Tommy Robredo | 636963.57 | 5 | 0.6 | 0.56 | 0.66 | 0.54 | 101.0 | 1.0 | 9.0 | 8.0 | 15.0 | 37.0 | 3 | 2 | 4 | 0.0476190476190476 | 0.523809523809524 | 0.5714285714285711 | 13.364467742966001 |
| Paolo Lorenzi | 351977.79 | 33 | 0.38 | 0.36 | 0.42 | 0.2 | 99.0 | 415.0 | 134.0 | 14.0 | 21.0 | 38.0 | 3 | 3 | 15 | 0.0714285714285714 | 0.0714285714285714 | 12.7713233559987 | |
| Ivo Karlovic | 468826.9 | 14 | 0.52 | 0.52 | 0.42 | 0.63 | 93.0 | 8.0 | 128.0 | 8.0 | 21.0 | 41.0 | 3 | 2 | 9 | 0.19047619047619 | 0.0476190476190476 | 0.38095238095238104 | 13.057988896144801 |
| Roger Federer | 5618777.87 | 1 | 0.82 | 0.83 | 0.76 | 0.87 | 16.0 | 7.0 | 4.0 | 6.0 | 16.0 | 38.0 | 3 | 2 | 9 | 3.08695652173913 | 0.4782608695652171 | 4.4782608695652195 | 15.5416247373677 |
| Guillermo Garcia Lopez | 470796.06 | 23 | 0.46 | 0.42 | 0.5 | 0.48 | 501.0 | 132.0 | 115.0 | 9.0 | 18.0 | 36.0 | 3 | 2 | 16 | 0.11764705882352902 | 0.17647058823529396 | 0.294117647058824 | 13.062180285599199 |
| Jo Wilfried Tsonga | 1379538.44 | 5 | 0.68 | 0.68 | 0.64 | 0.69 | 399.0 | 106.0 | 231.0 | 8.0 | 18.0 | 34.0 | 3 | 3 | 6 | 1.0625 | 0.0625 | 1.125 | 14.137259537419801 |
| Fernando Verdasco | 913358.47 | 7 | 0.57 | 0.54 | 0.61 | 0.55 | 291.0 | 64.0 | 73.0 | 8.0 | 17.0 | 36.0 | 2 | 3 | 4 | 0.10526315789473699 | 0.263157894736842 | 0.368421052631579 | 13.724883711215199 |
| Andreas Seppi | 587859.78 | 18 | 0.48 | 0.46 | 0.5 | 0.57 | 444.0 | 113.0 | 94.0 | 11.0 | 18.0 | 36.0 | 3 | 3 | 9 | 0.0555555555555556 | 0.0555555555555556 | 0.166666666666667 | 13.2842437290547 |
| Philipp Kohlschreiber | 674084.05 | 16 | 0.56 | 0.54 | 0.57 | 0.6 | 512.0 | 39.0 | 120.0 | 11.0 | 17.0 | 36.0 | 3 | 2 | 14 | 0.0526315789473684 | 0.315789473684211 | 0.421052631578947 | 13.421110085383699 |
| Teymuraz Gabashvili | 291151.07 | 43 | 0.37 | 0.36 | 0.39 | 0.27 | 71.0 | 596.0 | 23.0 | 15.0 | 15.0 | 34.0 | 3 | 3 | 12 | 12.5815975523401 | |||
| Rafael Nadal | 6294819.0 | 1 | 0.83 | 0.78 | 0.92 | 0.78 | 611.0 | 151.0 | 2.0 | 7.0 | 14.0 | 33.0 | 2 | 3 | 4 | 1.1578947368421102 | 3.1052631578947403 | 4.47368421052632 | 15.655237472068698 |
| Jurgen Melzer | 519159.4 | 8 | 0.51 | 0.51 | 0.52 | 0.53 | 190.0 | 77.0 | 12.0 | 12.0 | 17.0 | 38.0 | 3 | 3 | 2 | 0.2 | 0.05 | 0.25 | 13.159966244087999 |
| Dustin Brown | 264191.91 | 64 | 0.39 | 0.34 | 0.4 | 0.45 | 198.0 | 293.0 | 198.0 | 14.0 | 17.0 | 35.0 | 3 | 3 | 9 | 12.484431049859701 | |||
| Stan Wawrinka | 1877237.72 | 3 | 0.64 | 0.64 | 0.67 | 0.5 | 489.0 | 3.0 | 114.0 | 12.0 | 16.0 | 34.0 | 3 | 2 | 15 | 0.5 | 0.38888888888888895 | 0.8888888888888891 | 14.4453119564572 |
| Richard Gasquet | 953971.42 | 7 | 0.63 | 0.62 | 0.62 | 0.67 | 68.0 | 14.0 | 91.0 | 5.0 | 15.0 | 33.0 | 3 | 2 | 9 | 0.421052631578947 | 0.157894736842105 | 0.7894736842105259 | 13.7683889919104 |
| David Ferrer | 1749106.17 | 3 | 0.66 | 0.64 | 0.7 | 0.63 | 197.0 | 150.0 | 12.0 | 13.0 | 17.0 | 37.0 | 3 | 3 | 4 | 0.666666666666667 | 0.7222222222222221 | 1.5 | 14.3746154554174 |
| Go Soeda | 135495.27 | 47 | 0.38 | 0.37 | 0.31 | 0.24 | 249.0 | 133.0 | 200.0 | 35.0 | 3 | 3 | 3 | 11.816692010943502 | |||||
| Carlos Berlocq | 296433.93 | 37 | 0.41 | 0.33 | 0.46 | 0.25 | 292.0 | 364.0 | 10.0 | 11.0 | 18.0 | 37.0 | 3 | 2 | 4 | 0.14285714285714302 | 0.14285714285714302 | 12.5995796395367 | |
| Marcel Granollers | 772940.57 | 19 | 0.45 | 0.41 | 0.48 | 0.45 | 445.0 | 119.0 | 110.0 | 9.0 | 16.0 | 33.0 | 3 | 3 | 16 | 0.0714285714285714 | 0.214285714285714 | 0.28571428571428603 | 13.5579574423371 |
| Gilles Muller | 315361.79 | 21 | 0.52 | 0.53 | 0.46 | 0.56 | 305.0 | 280.0 | 60.0 | 16.0 | 17.0 | 36.0 | 2 | 3 | 6 | 0.0526315789473684 | 0.10526315789473699 | 12.661475798423199 | |
| Dudi Sela | 259822.33 | 29 | 0.42 | 0.45 | 0.19 | 0.48 | 214.0 | 49.0 | 138.0 | 7.0 | 16.0 | 34.0 | 3 | 2 | 6 | 12.4677533302564 | |||
| Daniel Gimeno Traver | 227631.36 | 48 | 0.36 | 0.25 | 0.42 | 0.1 | 619.0 | 12.0 | 75.0 | 9.0 | 18.0 | 34.0 | 3 | 3 | 4 | 12.3354827573315 | |||
| Julien Benneteau | 530930.11 | 25 | 0.48 | 0.49 | 0.41 | 0.47 | 149.0 | 18.0 | 115.0 | 14.0 | 18.0 | 38.0 | 3 | 3 | 3 | 13.182385671975801 | |||
| Novak Djokovic | 1 | 0.83 | 0.84 | 0.8 | 0.84 | 493.0 | 108.0 | 62.0 | 8.0 | 15.0 | 32.0 | 3 | 3 | 6 | 3.4705882352941204 | 0.823529411764706 | 4.64705882352941 | ||
| Yen Hsun Lu | 282170.35 | 33 | 0.42 | 0.42 | 0.24 | 0.44 | 351.0 | 2.0 | 103.0 | 9.0 | 17.0 | 36.0 | 3 | 3 | 6 | 12.5502662455528 | |||
| Viktor Troicki | 575913.2 | 12 | 0.52 | 0.53 | 0.51 | 0.52 | 181.0 | 449.0 | 126.0 | 5.0 | 20.0 | 34.0 | 3 | 3 | 2 | 0.2 | 0.2 | 13.263712233878 | |
| Florian Mayer | 485266.13 | 18 | 0.48 | 0.44 | 0.5 | 0.59 | 480.0 | 143.0 | 215.0 | 10.0 | 17.0 | 36.0 | 3 | 3 | 9 | 0.0666666666666667 | 0.133333333333333 | 13.0924527410764 | |
| Rogerio Dutra Silva | 166942.0 | 63 | 0.32 | 0.29 | 0.36 | 0.01 | 138.0 | 144.0 | 351.0 | 14.0 | 19.0 | 36.0 | 3 | 2 | 15 | 12.025401725685198 | |||
| Janko Tipsarevic | 506824.94 | 8 | 0.53 | 0.54 | 0.52 | 0.53 | 453.0 | 22.0 | 44.0 | 10.0 | 17.0 | 35.0 | 3 | 3 | 2 | 0.17647058823529396 | 0.0588235294117647 | 0.23529411764705901 | 13.1359209369523 |
| Ruben Ramirez Hidalgo | 167582.5 | 50 | 0.34 | 0.19 | 0.39 | 0.01 | 179.0 | 13.0 | 61.0 | 8.0 | 20.0 | 42.0 | 3 | 3 | 4 | 12.029231046304 | |||
| Mischa Zverev | 403370.93 | 25 | 0.4 | 0.41 | 0.32 | 0.5 | 35.0 | 26.0 | 444.0 | 12.0 | 17.0 | 32.0 | 2 | 3 | 9 | 0.0714285714285714 | 12.9076118394366 | ||
| Mikhail Youzhny | 713222.5 | 8 | 0.54 | 0.55 | 0.51 | 0.57 | 55.0 | 26.0 | 11.0 | 9.0 | 16.0 | 37.0 | 3 | 2 | 3 | 0.3 | 0.15 | 0.5 | 13.477548712426401 |
| Gael Monfils | 1054753.88 | 6 | 0.64 | 0.66 | 0.61 | 0.59 | 686.0 | 209.0 | 16.0 | 12.0 | 17.0 | 33.0 | 3 | 3 | 10 | 0.529411764705882 | 0.0588235294117647 | 0.588235294117647 | 13.8688180085766 |
| Andy Murray | 4102933.8 | 1 | 0.77 | 0.78 | 0.7 | 0.84 | 129.0 | 347.0 | 47.0 | 11.0 | 17.0 | 32.0 | 3 | 3 | 9 | 2.2666666666666697 | 0.2 | 3.06666666666667 | 15.227212836758499 |
| Marco Chiudinelli | 134908.0 | 52 | 0.35 | 0.35 | 0.26 | 0.4 | 16.0 | 109.0 | 33.0 | 10.0 | 18.0 | 38.0 | 3 | 3 | 3 | 11.812348343624999 | |||
| Marcos Baghdatis | 557432.31 | 8 | 0.56 | 0.57 | 0.43 | 0.58 | 376.0 | 38.0 | 104.0 | 3.0 | 17.0 | 34.0 | 3 | 3 | 6 | 0.1875 | 0.25 | 13.2310963579044 | |
| Gilles Simon | 869037.88 | 6 | 0.58 | 0.58 | 0.58 | 0.57 | 310.0 | 53.0 | 79.0 | 7.0 | 17.0 | 35.0 | 3 | 3 | 2 | 0.529411764705882 | 0.294117647058824 | 0.823529411764706 | 13.675141993631199 |
| Sergiy Stakhovsky | 314649.47 | 31 | 0.45 | 0.46 | 0.38 | 0.48 | 198.0 | 151.0 | 11.0 | 7.0 | 17.0 | 34.0 | 3 | 2 | 6 | 0.17647058823529396 | 0.23529411764705901 | 12.659214504542401 | |
| Simone Bolelli | 360726.07 | 36 | 0.43 | 0.36 | 0.48 | 0.52 | 354.0 | 19.0 | 123.0 | 6.0 | 17.0 | 34.0 | 3 | 2 | 16 | 12.7958741404096 | |||
| Stephane Robert | 218865.73 | 50 | 0.34 | 0.36 | 0.31 | 0.33 | 573.0 | 103.0 | 27.0 | 15.0 | 20.0 | 39.0 | 3 | 3 | 2 | 12.2962137157501 | |||
| Radek Stepanek | 597024.42 | 8 | 0.56 | 0.56 | 0.55 | 0.6 | 265.0 | 479.0 | 17.0 | 10.0 | 17.0 | 41.0 | 3 | 3 | 2 | 0.263157894736842 | 0.263157894736842 | 13.299713296060801 | |
| Jaroslav Pospisil | 179194.67 | 103 | 0.12 | 0.33 | 0.01 | 0.01 | 157.0 | 99.0 | 338.0 | 39.0 | 3 | 1 | 1 | 12.096228035777099 | |||||
| Lukasz Kubot | 590473.08 | 41 | 0.43 | 0.36 | 0.47 | 0.5 | 147.0 | 13.0 | 69.0 | 8.0 | 19.0 | 37.0 | 3 | 3 | 16 | 13.288679325096 | |||
| Jan Mertl | 300402.5 | 163 | 0.67 | 0.99 | 0.5 | 87.0 | 52.0 | 229.0 | 5.0 | 20.0 | 38.0 | 3 | 1 | 1 | 12.6128785210745 | ||||
| Daniel Munoz De La Nava | 138074.38 | 68 | 0.24 | 0.3 | 0.22 | 205.0 | 241.0 | 276.0 | 17.0 | 17.0 | 38.0 | 2 | 3 | 10 | 11.835547804446099 | ||||
| Frank Dancevic | 117914.62 | 65 | 0.38 | 0.38 | 0.05 | 0.48 | 233.0 | 30.0 | 17.0 | 4.0 | 18.0 | 35.0 | 3 | 2 | 3 | 11.6777160822304 | |||
| Lamine Ouahab | 38605.17 | 114 | 0.5 | 0.38 | 0.53 | 361.0 | 76.0 | 114.0 | 7.0 | 17.0 | 35.0 | 3 | 3 | 4 | 10.561141484307901 | ||||
| Giovanni Lapentti | 49029.0 | 110 | 0.34 | 0.46 | 0.24 | 0.33 | 505.0 | 142.0 | 149.0 | 3.0 | 19.0 | 37.0 | 3 | 3 | 10 | 10.8001672387612 | |||
| Fabio Fognini | 841913.38 | 9 | 0.54 | 0.48 | 0.59 | 0.51 | 415.0 | 58.0 | 152.0 | 15.0 | 16.0 | 32.0 | 3 | 3 | 4 | 0.0625 | 0.5 | 0.5625 | 13.643432413823302 |
| Flavio Cipolla | 203031.25 | 70 | 0.35 | 0.38 | 0.36 | 0.12 | 319.0 | 51.0 | 70.0 | 9.0 | 19.0 | 36.0 | 3 | 2 | 15 | 12.2211151870629 | |||
| Filippo Volandri | 263308.73 | 25 | 0.44 | 0.13 | 0.54 | 0.15 | 48.0 | 60.0 | 106.0 | 10.0 | 15.0 | 38.0 | 3 | 2 | 4 | 0.133333333333333 | 0.133333333333333 | 12.4810825010305 | |
| Santiago Giraldo | 61.57 | 28 | 0.45 | 0.39 | 0.51 | 0.43 | 390.0 | 152.0 | 34.0 | 8.0 | 18.0 | 32.0 | 3 | 3 | 4 | 4.12017473892312 | |||
| Adrian Menendez Maceiras | 199829.83 | 111 | 0.25 | 0.29 | 0.17 | 0.25 | 298.0 | 76.0 | 208.0 | 10.0 | 19.0 | 34.0 | 3 | 3 | 10 | 12.2052214333519 | |||
| Jan Hernych | 143583.67 | 59 | 0.4 | 0.42 | 0.32 | 0.48 | 93.0 | 35.0 | 34.0 | 11.0 | 18.0 | 40.0 | 3 | 3 | 9 | 11.8746732104669 | |||
| Maximo Gonzalez | 203559.91 | 58 | 0.32 | 0.19 | 0.37 | 0.01 | 50.0 | 250.0 | 265.0 | 7.0 | 18.0 | 36.0 | 3 | 3 | 4 | 12.2237156385726 | |||
| Michal Przysiezny | 103031.92 | 57 | 0.29 | 0.28 | 0.21 | 0.33 | 50.0 | 135.0 | 107.0 | 13.0 | 17.0 | 36.0 | 3 | 2 | 3 | 11.542794122114401 | |||
| Albert Montanes | 345078.82 | 22 | 0.47 | 0.3 | 0.53 | 0.32 | 109.0 | 13.0 | 3.0 | 11.0 | 18.0 | 39.0 | 3 | 3 | 4 | 0.3529411764705879 | 0.3529411764705879 | 12.7515281336877 | |
| Nicolas Almagro | 672014.62 | 9 | 0.59 | 0.47 | 0.66 | 0.47 | 106.0 | 582.0 | 53.0 | 8.0 | 17.0 | 34.0 | 3 | 2 | 4 | 0.8125 | 0.8125 | 13.418035375220999 | |
| Konstantin Kravchuk | 114634.22 | 78 | 0.26 | 0.22 | 0.5 | 0.2 | 28.0 | 295.0 | 2.0 | 12.0 | 19.0 | 35.0 | 3 | 3 | 14 | 11.649501642529 | |||
| Lleyton Hewitt | 1043996.7 | 1 | 0.7 | 0.7 | 0.64 | 0.76 | 6.0 | 1.0 | 16.0 | 3.0 | 17.0 | 39.0 | 3 | 3 | 9 | 1.0 | 0.1 | 1.5 | 13.8585668865002 |
| Tomas Berdych | 1734784.0 | 4 | 0.65 | 0.65 | 0.63 | 0.68 | 285.0 | 68.0 | 21.0 | 13.0 | 16.0 | 34.0 | 3 | 3 | 14 | 0.529411764705882 | 0.11764705882352902 | 0.7647058823529409 | 14.3663934679356 |
| Igor Sijsling | 216377.5 | 52 | 0.36 | 0.35 | 0.3 | 0.44 | 101.0 | 481.0 | 83.0 | 9.0 | 17.0 | 32.0 | 3 | 2 | 9 | 12.284779846426801 | |||
| Teodor Dacian Craciun | 218 | 141.0 | 253.0 | 51.0 | 9.0 | 17.0 | 39.0 | 3 | 3 | 1 | |||||||||
| Denis Istomin | 372861.12 | 33 | 0.47 | 0.46 | 0.45 | 0.54 | 662.0 | 4.0 | 30.0 | 8.0 | 17.0 | 33.0 | 3 | 3 | 9 | 0.0625 | 0.125 | 12.8289612968533 | |
| Steve Darcis | 220764.13 | 38 | 0.47 | 0.47 | 0.47 | 0.46 | 114.0 | 215.0 | 330.0 | 14.0 | 18.0 | 35.0 | 3 | 2 | 2 | 0.0666666666666667 | 0.0666666666666667 | 0.133333333333333 | 12.3048501254777 |
| Kevin Anderson | 1163846.71 | 5 | 0.59 | 0.61 | 0.53 | 0.59 | 101.0 | 249.0 | 296.0 | 11.0 | 20.0 | 33.0 | 3 | 3 | 6 | 0.42857142857142894 | 0.42857142857142894 | 13.9672412061614 | |
| Dmitry Tursunov | 394675.0 | 20 | 0.51 | 0.52 | 0.4 | 0.57 | 146.0 | 146.0 | 222.0 | 6.0 | 17.0 | 37.0 | 3 | 3 | 3 | 0.33333333333333304 | 0.46666666666666706 | 12.8858179203999 | |
| Michael Berrer | 212823.15 | 42 | 0.38 | 0.41 | 0.3 | 0.29 | 127.0 | 152.0 | 26.0 | 11.0 | 18.0 | 39.0 | 2 | 2 | 10 | 12.2682168181267 | |||
| Tobias Kamke | 216612.27 | 64 | 0.38 | 0.37 | 0.36 | 0.46 | 93.0 | 271.0 | 235.0 | 7.0 | 17.0 | 33.0 | 3 | 3 | 9 | 12.285864260144 | |||
| Paul Henri Mathieu | 370534.88 | 12 | 0.48 | 0.46 | 0.49 | 0.42 | 125.0 | 114.0 | 47.0 | 9.0 | 17.0 | 38.0 | 3 | 3 | 3 | 0.11764705882352902 | 0.23529411764705901 | 12.822702862337 | |
| Frederico Gil | 145393.3 | 62 | 0.47 | 0.39 | 0.55 | 0.12 | 344.0 | 125.0 | 10.0 | 8.0 | 17.0 | 34.0 | 3 | 3 | 4 | 11.8871977632399 | |||
| Malek Jaziri | 294278.0 | 42 | 0.41 | 0.42 | 0.43 | 0.3 | 168.0 | 201.0 | 158.0 | 16.0 | 19.0 | 36.0 | 3 | 3 | 15 | 12.5922801777746 | |||
| Ernests Gulbis | 453547.06 | 10 | 0.51 | 0.5 | 0.52 | 0.38 | 277.0 | 80.0 | 8.0 | 10.0 | 15.0 | 31.0 | 3 | 3 | 3 | 0.3125 | 0.0625 | 0.375 | 13.024854313826099 |
| Sam Querrey | 794143.47 | 11 | 0.56 | 0.56 | 0.45 | 0.64 | 485.0 | 67.0 | 24.0 | 12.0 | 18.0 | 32.0 | 3 | 3 | 9 | 0.5333333333333329 | 0.0666666666666667 | 0.666666666666667 | 13.5850194166015 |
| Blaz Kavcic | 163640.09 | 68 | 0.39 | 0.37 | 0.42 | 0.2 | 458.0 | 60.0 | 106.0 | 7.0 | 18.0 | 33.0 | 3 | 3 | 15 | 12.005424722031 | |||
| Toshihide Matsui | 98480.67 | 261 | 0.67 | 0.6 | 237.0 | 72.0 | 223.0 | 41.0 | 3 | 3 | 1 | 11.4976155642471 | |||||||
| Juan Monaco | 577459.79 | 10 | 0.56 | 0.46 | 0.63 | 0.39 | 315.0 | 146.0 | 251.0 | 10.0 | 17.0 | 35.0 | 3 | 3 | 4 | 0.0714285714285714 | 0.5714285714285711 | 0.6428571428571429 | 13.2663940912483 |
| Robin Haase | 508178.29 | 33 | 0.46 | 0.44 | 0.51 | 0.4 | 502.0 | 53.0 | 2.0 | 7.0 | 17.0 | 32.0 | 3 | 3 | 4 | 0.14285714285714302 | 0.14285714285714302 | 13.1385876295539 | |
| Michael Russell | 156858.0 | 60 | 0.34 | 0.37 | 0.26 | 0.3 | 68.0 | 70.0 | 345.0 | 9.0 | 19.0 | 41.0 | 3 | 3 | 10 | 11.9630962164622 | |||
| Jimmy Wang | 87971.23 | 85 | 0.46 | 0.46 | 0.29 | 0.39 | 516.0 | 197.0 | 26.0 | 5.0 | 16.0 | 35.0 | 3 | 3 | 3 | 11.3847651081883 | |||
| Lukas Lacko | 232969.07 | 44 | 0.4 | 0.42 | 0.2 | 0.42 | 190.0 | 92.0 | 186.0 | 8.0 | 17.0 | 32.0 | 3 | 3 | 6 | 12.358660976955099 | |||
| Tommy Haas | 680499.35 | 2 | 0.63 | 0.64 | 0.59 | 0.63 | 15.0 | 3.0 | 6.0 | 6.0 | 17.0 | 41.0 | 3 | 2 | 2 | 0.55 | 0.1 | 0.75 | 13.430582145893199 |
| Pablo Andujar | 411965.85 | 32 | 0.41 | 0.29 | 0.51 | 0.12 | 611.0 | 146.0 | 69.0 | 11.0 | 18.0 | 34.0 | 3 | 3 | 4 | 0.307692307692308 | 0.307692307692308 | 12.9286957365467 | |
| Adrian Mannarino | 531070.77 | 22 | 0.46 | 0.46 | 0.26 | 0.59 | 457.0 | 122.0 | 190.0 | 14.0 | 15.0 | 31.0 | 2 | 3 | 9 | 0.0769230769230769 | 13.1826505681797 | ||
| Matthias Bachinger | 142133.73 | 85 | 0.36 | 0.39 | 0.37 | 0.22 | 316.0 | 159.0 | 52.0 | 6.0 | 17.0 | 32.0 | 3 | 3 | 15 | 11.8645236539685 | |||
| Lukas Rosol | 300705.64 | 26 | 0.44 | 0.39 | 0.52 | 0.4 | 328.0 | 17.0 | 89.0 | 10.0 | 18.0 | 34.0 | 3 | 3 | 4 | 0.0714285714285714 | 0.0714285714285714 | 0.14285714285714302 | 12.613887125036198 |
| Jeremy Chardy | 577229.53 | 25 | 0.5 | 0.48 | 0.53 | 0.48 | 303.0 | 69.0 | 117.0 | 8.0 | 18.0 | 33.0 | 3 | 3 | 2 | 0.0666666666666667 | 0.0666666666666667 | 13.2659952653493 | |
| Matteo Viola | 123883.8 | 118 | 0.24 | 0.33 | 0.01 | 0.01 | 142.0 | 154.0 | 402.0 | 9.0 | 16.0 | 32.0 | 3 | 3 | 10 | 11.727099308463302 | |||
| Marc Fornell Mestres | 236 | 0.01 | 0.01 | 94.0 | 178.0 | 66.0 | 38.0 | 3 | 1 | 1 | |||||||||
| Pablo Cuevas | 530023.94 | 19 | 0.53 | 0.41 | 0.6 | 0.41 | 480.0 | 124.0 | 117.0 | 12.0 | 18.0 | 34.0 | 3 | 2 | 4 | 0.375 | 0.375 | 13.1806774543195 | |
| Potito Starace | 315379.17 | 27 | 0.46 | 0.31 | 0.53 | 0.08 | 84.0 | 200.0 | 33.0 | 6.0 | 19.0 | 38.0 | 3 | 3 | 4 | 12.6615309082103 | |||
| Victor Hanescu | 306932.21 | 26 | 0.45 | 0.34 | 0.54 | 0.41 | 265.0 | 40.0 | 102.0 | 10.0 | 17.0 | 38.0 | 3 | 2 | 4 | 0.0714285714285714 | 0.0714285714285714 | 12.634382187854 | |
| Ivo Klec | 68838.17 | 184 | 0.22 | 0.2 | 0.25 | 282.0 | 309.0 | 264.0 | 7.0 | 18.0 | 39.0 | 3 | 3 | 1 | 11.1395136665904 | ||||
| Leonardo Mayer | 499417.46 | 21 | 0.48 | 0.43 | 0.53 | 0.46 | 453.0 | 67.0 | 64.0 | 12.0 | 15.0 | 32.0 | 3 | 2 | 4 | 0.153846153846154 | 0.153846153846154 | 13.121197618171001 | |
| Carlos Salamanca | 55554.83 | 137 | 0.38 | 0.01 | 0.75 | 197.0 | 48.0 | 446.0 | 9.0 | 18.0 | 37.0 | 2 | 3 | 1 | 10.9251257399828 | ||||
| Donald Young | 308544.0 | 38 | 0.4 | 0.42 | 0.22 | 0.38 | 59.0 | 394.0 | 38.0 | 8.0 | 14.0 | 30.0 | 2 | 3 | 6 | 12.639619737765301 | |||
| Alejandro Falla | 193833.19 | 50 | 0.4 | 0.39 | 0.43 | 0.39 | 291.0 | 148.0 | 104.0 | 12.0 | 16.0 | 36.0 | 2 | 3 | 2 | 12.1747532228056 |
Διαχείριση κενών τιμών
Συμπλήρωση των κενών τιμών
#clear the R environment
rm(list = ls())
#load the MissForest R library to impute the dataset
library(missForest)
#read data for imputation
cleaned_data = read.csv("cleaned_raw_data.csv")
#remove some unused variables
mydata = cleaned_data[,2:6,8:10]
#log and logit transformations when needed
mydata[,c(1:2)] = log(mydata[,1:2])
mydata[,c(3:5)] =log(mydata[,c(3:5)]/(1-mydata[,c(3:5)]))
#impute missing values
mydata.imp <- missForest(mydata)$ximpΣυγκεκριμένα, προκειμένου οι υπολειπόμενες κενές τιμές του dataset να συμπληρωθούν, χρησιμοποιήθηκε το πακέτο missForest της R (βλ. MissForest —non-parametric missing value imputation for mixed-type data). Πρόκειται για μέθοδο μηχανικής μάθησης με βάση τον αλγόριθμο Random Forest, ο οποίος θα μπορούσε, πολύ συνοπτικά, να περιγραφεί ως μια σειρά από συνδυαζόμενα «δέντρα αποφάσεων» («decision trees»).
Όσον αφορά στον Random Forest, ένα πολύ απλό παράδειγμα είναι το εξής: έστω ότι έχουμε ένα δείγμα ανθρώπων, των οποίων το φύλο δεν γνωρίζουμε (ελλείπουσα τιμή) και θέλουμε να το προβλέψουμε, έχοντας καταγεγραμμένα το ύψος και το βάρος τους. Για αυτήν την απλή υπόθεση εργασίας, μπορούμε να φτιάξουμε ένα «δέντρο απόφασης» («decision tree»), με δύο «παρακλάδια»: Το πρώτο ρωτά το ύψος κάθε ατόμου και, αν το ύψος είναι μεγαλύτερο από 1,80 μ., το άτομο κατηγοριοποιείται ως «άντρας». Αντίθετα, εάν είναι μικρότερο από 1,80 μ., το δεύτερο παρακλάδι ρωτά το βάρος του ατόμου, πριν από τη λήψη απόφασης: εάν το άτομο έχει βάρος λιγότερο από 70 κιλά, ταξινομείται ως «γυναίκα». Σε πραγματική εφαρμογή και σε πιο σύνθετα παραδείγματα, το πλήθος των διακλαδώσεων αυξάνεται και μεγάλος αριθμός «δέντρων αποφάσεων» συνδυάζονται για την τελική πρόβλεψη.
Στην περίπτωση των κενών παρατηρήσεων, ουσιαστικά, καταλήγουμε σε εκτιμώμενες τιμές, με τις οποίες οι κενές συμπληρώνονται, εκπαιδεύοντας τον αλγόριθμο με τη χρήση υφιστάμενων δεδομένων. Στο εν λόγω dataset, στο οποίο βασίζεται η στατιστική ανάλυση για το συγκεκριμένο θέμα, έχουμε κοινή λίστα χαρακτηριστικών για κάθε παίκτη (θέσεις στην κατάταξη, αμοιβές βραβείων, «backhand», αγαπημένο είδος γηπέδου, επαγγελματική ηλικία κ.ο.κ). Κάθε χαρακτηριστικό είναι μία μεταβλητή, δηλαδή μία στήλη στο dataset.
Έστω ότι μας λείπουν δεδομένα για τις αμοιβές ενός αθλητή a από βραβεία, έχουμε:
- κενές τιμές για αμοιβές βραβείων που έχει λάβει ο αθλητής a
- υπάρχουσες τιμές για άλλα χαρακτηριστικά του αθλητή a
- υφιστάμενες τιμές για κάποια από τα χαρακτηριστικά της λίστας, στην περίπτωση άλλων αθλητών
- κενές τιμές για κάποια άλλα χαρακτηριστικά της λίστας, στην περίπτωση άλλων αθλητών
Ταξινομούμε τα χαρακτηριστικά των παικτών (μεταβλητές), με βάση τον αριθμό των κενών τιμών που παρουσιάζουν, σε αύξουσα σειρά –δηλαδή από εκείνο με τα πιο πλήρη δεδομένα προς εκείνο με τα πιο ελλιπή δεδομένα.
Με βάση αυτήν την ταξινόμηση, για κάθε παίκτη x, για κάθε χαρακτηριστικό του (μεταβλητή), οι τυχόν κενές τιμές συμπληρώνονται με τη χρήση ενός αλγόριθμου Random Forest, ο οποίος βασίζεται: α) στις υπάρχουσες τιμές για τα υπόλοιπα χαρακτηριστικά του αθλητή x και β) στις υπάρχουσες τιμές άλλων παικτών για το χαρακτηριστικό που ο αθλητής x εμφανίζει κενή τιμή. Ανάλογη διαδικασία εφαρμόζεται για κάθε μεταβλητή που παρουσιάζει κενές τιμές και η διαδικασία επαναλαμβάνεται πολλές φορές, έως ότου πληροί συγκεκριμένα κριτήρια απόδοσης.
Εύρεση ομοιότητας μεταξύ αθλητών
Κατηγοριοποίηση παικτών σε ομάδες ομοιότητας και επιλογή του «cluster» Τσιτσιπά
#clear the R environment
rm(list = ls())
#load R libraries
library(missForest)
library(KRLS)#to compute RBF
library(irlba) #to compute partial eigen decomposition
library(spam)#to facilitate linear algebra computations
library(spam64)#to facilitate linear algebra computations
#read and clean the data
cleaned_data = read.csv("cleaned_raw_data.csv")
names = cleaned_data$names
mydata = cleaned_data[,2:6,8:10]
#log and logit transformations
mydata[,c(1:2)] = log(mydata[,1:2])
mydata[,c(3:5)] =log(mydata[,c(3:5)]/(1-mydata[,c(3:5)]))
#impute missing values
mydata.imp <- missForest(mydata)$ximp
#compute similarity matrix
mysimils =gausskernel(mydata.imp, sigma=1) #introduce sparsity to facilitate linear algebra computations by setting low similarities equal to 0
mysimils[which(mysimils<=10^(-5))]=0
#compute regularized Laplacian of similarity matrix
diag(mysimils) =0
N= dim(mysimils)[1]
DD = rep(NA,N)
for(i in 1:N) DD[i] = sum(mysimils[i,])
DD = DD + mean(DD)
myd =diag.spam(1/sqrt(DD))
tSimils =myd%*%mysimils%*%myd
#compute partial spectral decomposition of Laplacian
K=150
myeigen = partial_eigen(as.dgCMatrix.spam(tSimils), n =K, symmetric = TRUE)
U = myeigen$vectors
#normalize eigenvectors to have unit length
scalar1 <- function(x) {x / sqrt(sum(x^2))}
Ustar = matrix(NA,dim(U)[1],dim(U)[2])
for(i in 1:dim(U)[1]){
Ustar[i,] = scalar1(U[i,])
#run k-means
km = kmeans(Ustar,centers = 150,iter.max = 1000)
#find Tsitsipas cluster
size_clsts = km$size
clsts = which(size_clsts>=2)
same_players =list()
tsitsipas_clst=rep(0,length(clsts))
for(i in 1:length(clsts)){
same_players[[i]] = which( km$cluster==clsts[i] )
if(length( intersect(same_players[[i]],which(names=="Stefanos Tsitsipas")))>0)
{
tsitsipas_clst[i] = 1
}
}
select_tsitsip_clst = same_players[[which(tsitsipas_clst>0)]]
select_tsitsip_clst=select_tsitsip_clst[-5] #we exclude the fifth member of the cluster because he seems to be an outlier due to two injuries that he had and he stopped and started again
tsitsipas_clst_data = cleaned_data[select_tsitsip_clst,]
tsitsipas_clst_names = names[select_tsitsip_clst]
Μετά τη συμπλήρωση των κενών τιμών, το dataset των 1.602 σειρών (κάθε παίκτης, μία σειρά) και 20 στηλών (κάθε στήλη, ένα χαρακτηριστικό των αθλητών) είναι πλήρες. Για κάθε δυνατό ζεύγος παικτών, υπολογίζεται ένας δείκτης ομοιότητας μεταξύ τους, με την εφαρμογή της «ακτινικής συνάρτησης βάσης» (RBF kernel). Αυτός ο δείκτης είναι ένας θετικός αριθμός που δηλώνει τον βαθμό ομοιότητας ανάμεσα σε έναν αθλητή και στον εκάστοτε άλλο παίκτη του dataset.
Δημιουργείται, έτσι, ένα «πλέγμα ομοιότητας» (similarity matrix), δηλαδή ένας πίνακας ο οποίος περιλαμβάνει τον εν λόγω δείκτη ομοιότητας για κάθε ζεύγος αθλητών. Πρόκειται για έναν πίνακα διαστάσεων 1.602 x 1.602 –σειρές και στήλες αντιστοιχούν στους παίκτες μελέτης, σχηματίζοντας, έτσι, τα πιθανά ζεύγη αθλητών: σε κάθε κελί του «similarity matrix», υπάρχει μία τιμή η οποία αντιστοιχεί στον δείκτη ομοιότητας ανάμεσα στους εκάστοτε δύο τενίστες αναφοράς.
Ακολούθως, προκειμένου οι παίκτες οι οποίοι μοιάζουν μεταξύ τους να κατηγοριοποιηθούν ανά ομάδες, υιοθετούμε την τεχνική της «ανάλυσης συστάδων» (cluster analysis) και, συγκεκριμένα, την τεχνική της «φασματικής ομαδοποίησης» (spectral clustering) –το «similiarity matrix» είναι αρκετά μεγάλο (1.602 x 1.602) και, άρα, θα διευκόλυνε να εργαστούμε με έναν πίνακα μικρότερων διαστάσεων, ο οποίος, όμως, θα περιέχει την περισσότερη δυνατή πληροφορία από το αρχικό «similarity matrix».
Ακολουθούμε τα παρακάτω βήματα:
- Μετασχηματισμός αρχικού «similarity matrix» σε κανονικοποιημένο πίνακα Laplace
- Ανάλυση πίνακα Laplace σε κύριες συνιστώσες (spectral decomposition)
- Ομαδοποίηση των γραμμών (παικτών) του αρχικού «similarity matrix», εφαρμόζοντας τον k-means αλγόριθμο στο παραγόμενο αποτέλεσμα του «spectral decomposition»
Καταλήγουμε με 150 ομάδες («clusters») όμοιων παικτών και επιλέγουμε εκείνη στην οποία ανήκει ο Στέφανος Τσιτσιπάς, προκειμένου να δουλέψουμε τις προβλέψεις για την πορεία του στην παγκόσμια κατάταξη.
Μάλιστα, στην ομάδα Τσιτσιπά, ο οποίος μετρά πέντε χρόνια επαγγελματικής σταδιοδρομίας, έχουν συμπεριληφθεί παίκτες με τουλάχιστον 15 χρόνια καριέρας. Αυτό είναι κρίσιμης σημασίας για τη μέθοδο των προβλέψεων, ακριβώς διότι η τεχνική μας για τις προβλέψεις βασίζεται σε ήδη υφιστάμενες επαγγελματικές διαδρομές όμοιων αθλητών.
Η μέθοδος των προβλέψεων
Με δεδομένο ότι το ερευνητικό ερώτημα είναι ποιες θέσεις ο Στέφανος Τσιτσιπάς μπορεί να κατέχει στην παγκόσμια κατάταξη στο μέλλον και ότι ο ίδιος έχει, ως στιγμής, πενταετή πορεία, δημιουργείται μοντέλο πρόβλεψης, με ορίζοντα δεκαετίας, εφαρμόζοντας τη στατιστική τεχνική του δειγματικού μέσου.
Προβλέπουμε τις επιδόσεις του αθλητή, για τα επόμενα δέκα χρόνια, με βάση τον μέσο όρο πραγματικών επιδόσεων όμοιων παικτών, οι οποίοι, όμως, έχουν περισσότερα χρόνια καριέρας.
Χρησιμοποιούμε, δηλαδή, τα πραγματικά δεδομένα κατάταξης των ομοίων του Τσιτσιπά από την εποχή που διένυαν τη δεύτερη και την τρίτη πενταετία της καριέρας τους, προκειμένου να προβούμε σε εκτιμήσεις για την πορεία Τσιτσιπά τα επόμενα δέκα χρόνια.
Προκειμένου ο δειγματικός μέσος (δηλαδή, η πρόβλεψή μας) να μην επηρεάζεται από τυχόν ακραίες τιμές και παρά το γεγονός ότι η ομάδα Τσιτσιπά αποτελείται από μόλις δέκα μέλη (τον ίδιο και ακόμη εννέα παίκτες), αναζητούμε υπο-ομάδες όμοιων αθλητών εντός της κατηγορίας στην οποία έχει ενταχθεί ο Στέφανος Τσιτσιπάς. Μετρώντας την ευκλείδεια απόσταση κάθε παίκτη από το κέντρο του «cluster» (όπως αυτό υπολογίζεται από τον ίδιο τον αλγόριθμο k-means), βρίσκουμε:
- υπο-ομάδα αθλητών α’ που βρίσκεται μακρύτερα του κέντρου του «cluster» –πρόκειται για παίκτες οι οποίοι παρουσιάζουν ελαφρώς καλύτερη κατάταξη από τον μέσο όρο των θέσεων που έχουν κατακτήσει οι αθλητές της κατηγορίας την εκάστοτε αγωνιστική σεζόν τους. Σε αυτήν την υπο-ομάδα α’, εμφανίζεται και ο Στέφανος Τσιτσιπάς.
- υπο-ομάδα αθλητών β’ που είναι κοντά στο κέντρο του «cluster» –δηλαδή, οι θέσεις τους στην παγκόσμια κατάταξη δεν απέχουν πολύ από τον μέσο όρο των θέσεων που έχουν επιτύχει όλοι οι παίκτες της κατηγορίας την εκάστοτε αγωνιστική σεζόν τους
Με αυτό το δεδομένο, επιλέγονται αθλητές του «cluster» Τσιτσιπά από τις δύο διαφορετικές υπο-ομάδες, για δοκιμαστικές εφαρμογές του μοντέλου πρόβλεψης: με τη χρήση των δεδομένων τους από την πρώτη πενταετία της καριέρας τους, κάνουμε «ψευδοπροβλέψεις» για τα επόμενα έτη της επαγγελματικής διαδρομής τους, τις οποίες συγκρίνουμε με τα πραγματικά δεδομένα των θέσεών τους στην παγκόσμια κατάταξη. Κατ’ αυτόν τον τρόπο, προκύπτει και το περιθώριο λάθους των προβλέψεών μας.
Συγκεκριμένα, για τους σκοπούς της δοκιμαστικής εφαρμογής του μοντέλου, επιλέγονται:
- ο Αλεξάντερ Ζβέρεφ, ο οποίος, παρά το γεγονός ότι μετρά μόλις επτά χρόνια επαγγελματικής καριέρας, ανήκει στην υπο-ομάδα α’ (όπως ο Στέφανος Τσιτσιπάς). Παρουσιάζει, επίσης, ιδιαίτερα όμοια πορεία με τον Τσιτσιπά και σήμερα αποτελεί έναν από τους βασικούς ανταγωνιστές του.
- οι Σταν Βαβρίνκα, Νταβίντ Φερέρ και Τόμας Μπέρντιχ, οι οποίοι, αφενός, έχουν περισσότερα από 15 χρόνια επαγγελματικής πορείας και, αφετέρου, ανήκουν στην υπο-ομάδα β’
Για τον Ζβέρεφ (υπο-ομάδα α’), η δοκιμή εφαρμόζεται με τη χρήση δειγματικού μέσου που προκύπτει μόνο από τις θέσεις των τεσσάρων αθλητών του «cluster», οι οποίοι εμφανίζουν τις καλύτερες θέσεις στην κατάταξη την εκάστοτε αγωνιστική σεζόν τους. Για τους Βαβρίνκα, Φερέρ και Μπέρντιχ (υπο-ομάδα β’), οι «ψευδοπροβλέψεις» γίνονται με τον υπολογισμό του δειγματικού μέσου επί του συνόλου των δεδομένων των παικτών του «cluster» την εκάστοτε αγωνιστική σεζόν εμφάνισης.
Όπως φαίνεται στο παρακάτω γράφημα, οι πραγματικές θέσεις κατάταξης των αθλητών συνήθως βρίσκονται μέσα στα όρια των προβλέψεων που κάνει το μοντέλο μας.
Για τις προβλέψεις των θέσεων που ο Στέφανος Τσιτσιπάς μπορεί να κατέχει στην παγκόσμια κατάταξη την επόμενη δεκαετία, επιλέγεται ο τρόπος της πρόβλεψης που εφαρμόστηκε στην πολύ όμοια περίπτωση Ζβέρεφ: για τον υπολογισμό του δειγματικού μέσου, οι παίκτες με χαμηλότερες θέσεις κατάταξης από τη διάμεσο του «cluster» εξαιρούνται και το μοντέλο λαμβάνει υπόψη του τις θέσεις των παικτών με τις καλύτερες επιδόσεις κάθε φορά.
Κοιτώντας πιο προσεκτικά την περίπτωση Ζβέρεφ και στον βαθμό που ο επιλεγμένος τρόπος υπολογισμού των προβλέψεων επηρεάζει την εκτιμώμενη πορεία Τσιτσιπά, αξίζει να σημειωθεί το εξής: Ενώ ο Ζβέρεφ είχε επιτύχει την τέταρτη θέση στην κατάταξη κατά την έκτη αγωνιστική σεζόν του, το μοντέλο προβλέπει την 11η θέση (μέση εκτίμηση) για τον ίδιο κατά την αντίστοιχη περίοδο, η οποία είναι και η πρώτη σεζόν πρόβλεψης. Αντίθετα, τις επόμενες σεζόν, το μοντέλο πρόβλεψης «ευθυγραμμίζεται» με τα πραγματικά επιτεύγματα Ζβέρεφ. Η «αστοχία» της πρώτης πρόβλεψης εξηγείται, εάν κανείς λάβει υπόψη του ότι η πορεία του Ζβέρεφ είναι όμοια με εκείνη των υπολοίπων παικτών του γκρουπ μετά την τρίτη αγωνιστική σεζόν της καριέρας του. Η ραγδαία ανέλιξη στην παγκόσμια κατάταξη, την οποία οι Ζβέρεφ και Τσιτσιπάς είχαν τα πρώτα χρόνια της διαδρομής τους, δεν παρατηρείται αντίστοιχα στην περίπτωση των κατά τα άλλα όμοιων αθλητών, δεδομένα των οποίων, όμως, «τροφοδοτούν» το μοντέλο και επηρεάζουν την εκτιμώμενη τιμή κατά την πρώτη σεζόν πρόβλεψης.
Σημειώνεται, επίσης, ότι η δημιουργία ενός πολυμεταβλητού μοντέλου θα ήταν χρήσιμη, για ακόμα περισσότερο ρεαλιστικές προβλέψεις σε ανάλογο εγχείρημα στο μέλλον: στο τένις, η πορεία του αθλητή εξαρτάται σημαντικά από τη διαδρομή των αντιπάλων του. Με το παρόν μοντέλο, υφίσταται η υπόθεση εργασίας ότι ένας παίκτης p θα ακολουθήσει πορεία όμοια με τους n ομοίους του, χωρίς να είναι δεδομένο ότι οι αντίπαλοί του θα έχουν επιδόσεις όμοιες με εκείνες των αντιπάλων των ομοίων n που εδώ λαμβάνονται υπόψη.
Οπτικοποίηση δεδομένων
Η δημιουργία των γραφημάτων που οπτικοποιούν τη στατιστική ανάλυση των δεδομένων έγινε με χρήση της γλώσσας προγραμματισμού Python και της στατιστικής γλώσσας προγραμματισμού R.
Συγκεκριμένα, για τη δημιουργία των διαδραστικών γραφημάτων, χρησιμοποιήθηκε η βιβλιοθήκη Plotly Python Open Source Graphing Library, ενώ τα στατικά γραφήματα δημιουργήθηκαν με τη χρήση του πακέτου ggplot2 σε R.
Ειδικά η οπτικοποίηση της ομάδας («cluster») Τσιτσιπά και της ομοιότητας μεταξύ των παικτών της επιλέχθηκε να γίνει με αραχνοειδές διάγραμμα (στα αγγλικά, λεγόμενο ως «spider plot», «radar plot» ή «polar plot»): το «radar plot» ενδείκνυται για τη συγκριτική οπτικοποίηση πολλαπλών (ποσοτικών) μεταβλητών σε δισδιάστατη μορφή. Ιδίως όταν οπτικοποιούνται περισσότερες από μία περιπτώσεις μελέτης, το σχήμα του «radar plot» είναι που εξυπηρετεί την οπτική σύγκριση. Στο πλαίσιο του συγκεκριμένου θέματος, όσο πιο πολύ μοιάζουν τα σχήματα των παικτών, τόσο πιο όμοιοι είναι οι αθλητές μεταξύ τους. Ωστόσο, το «radar plot» μπορεί να γίνει εξαιρετικά «δυσανάγνωστο», όταν υπάρχουν πολλά επικαλυπτόμενα σχήματα –όπως και εδώ, όπου η ανάγκη ήταν να οπτικοποιηθούν δεδομένα τουλάχιστον δέκα αθλητών («cluster» Τσιτσιπά). Για τον λόγο αυτό, επιλέχθηκε ο διαδραστικός σχεδιασμός, προκειμένου να είναι η εφικτή η αποεπιλογή παικτών ή η επιλογή συγκεκριμένων αθλητών προς σύγκριση.
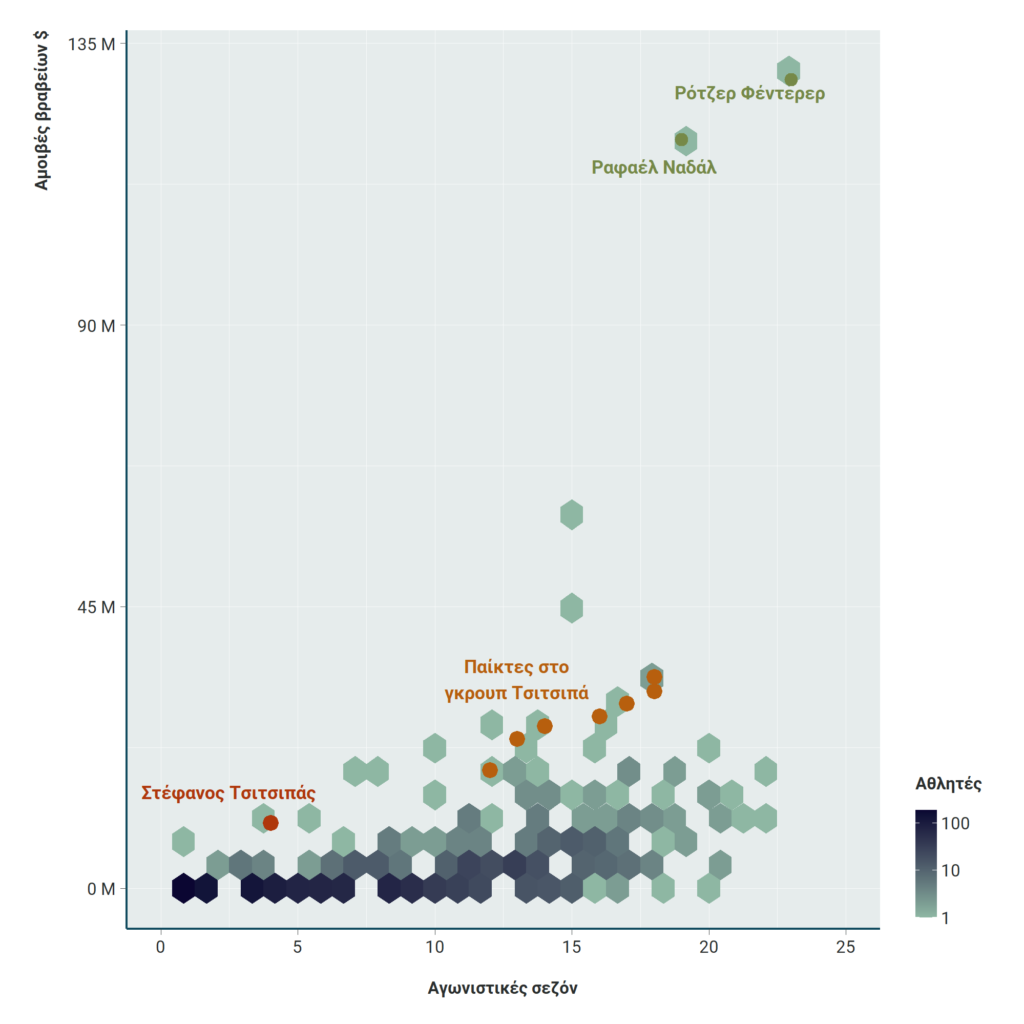
Για την οπτικοποίηση της κατανομής των 1.602 παικτών του dataset με βάση, για παράδειγμα, τα κέρδη τους σε σχέση με τις αγωνιστικές σεζόν τους, επιλέχθηκε το «εξαγωνικό πλέγμα» (στα αγγλικά, λεγόμενο ως «hexagonal binning», «hexbin plot» κλπ): το «hexbin plot» είναι μια προσέγγιση διαφορετική του διαγράμματος διασποράς (scatterplot), το οποίο συνήθως επιλέγεται για την οπτικοποίηση της σχέσης μεταξύ δύο ποσοτικών μεταβλητών. Όταν τα δεδομένα είναι τόσο πολλά, ώστε οι συνεχείς επικαλύψεις να μην αποδίδουν τη μέγιστη δυνατή πληροφορία, το «hexbin plot» ενδείκνυται, καθώς αποτυπώνει τη συγκέντρωση δεδομένων μέσα στα εξαγωνικά πλέγματα: εν προκειμένω, όσο πιο σκούρο μπλε είναι το χρώμα κάθε «hexbin», τόσο περισσότεροι αθλητές συγκεντρώνονται στο σημείο.
Το παρόν είναι αποτέλεσμα συνεργασίας του iMEdD Lab με την ερευνητική ομάδα AUEB Sports Analytics Group, στόχος της οποίας είναι η προαγωγή της υλοποίησης ποσοτικής ανάλυσης υψηλού επιπέδου στα σπορ, σε ακαδημαϊκό και επαγγελματικό επίπεδο. Η ομάδα εργάζεται στον τομέα των λεγόμενων «Sports Analytics», περιλαμβανομένων θεμάτων όπως η δημιουργία στατιστικών μοντέλων και η πρόβλεψη αθλητικών αποτελεσμάτων, τα οικονομικά των σπορ, η ανάλυση απόδοσης, η οπτικοποίηση και η μέτρηση της ανταγωνιστικής ισορροπίας.